Внутреннее внешнее сопротивление
Внутреннее и внешнее сопротивление регулируется таким образом, чтобы разность потенциалов в ячейке составляла 6 — 7 в. Если электролиз продолжается слишком долго, то наступает резкое увеличение вольтажа, заметное выделение газа на поверхности катода и разложение амальгамы при взаимодействии с оставшимся электролитом. Это явление может возникнуть также вследствие образования кристаллов амальгамы бария, образующих корку на поверхности катода.
|
Щитовые милливольтметры М-64 с профильной шкалой.| Внешний вид и принципиальная схема самопишущего милливольтметра. |
Причиной этой недостаточной точности является влияние окружающей среды на показания внутреннего и внешнего сопротивления цепи. Такие явления устраняются при использовании в пирометрах в качестве измерительного прибора потенциометра.
Мощность, развиваемая автомобильным дви — 1ателем, расходуется на преодоление внутренних и внешних сопротивлений движению; на фиг.
|
Структурная схема автоматического компенсатора напря. |
Для компенсации напряжения необходимо высокое входное сопротивление, благодаря чему достигается независимость работы прибора от внутренних и внешних сопротивлений измерительной цепи. Выходные величины автоматических приборов уравновешивания могут быть представлены в виде механических перемещений регистрирующего органа или в виде напряжения и тока.
|
Внутренние сопротивления двигателей постоянного тока. |
На рис. 2 — 2 показаны схемы включения в сеть двигателей параллельного, последовательного и смешанного возбуждения с обозначенными внутренними и внешними сопротивлениями.
Процесс торможения механизма передвижения состоит в преодолении сил инерции его поступательно движущихся и вращающихся элементов за счет момента, развиваемого тормозом, и момента от всех внутренних и внешних сопротивлений. Остановка механизмов передвижения без тормозов только под действием внешних и внутренних сопротивлений применяется крайне редко и в основном при использовании ручного привода или для тихоходных кранов. Необходимость установки тормозов на механизмах передвижения кранов и тележек со скоростями движения более 32 м / мин указана в Правилах Госгортехнадзора.
|
Графики зависимости величины, представляющей правую часть уравнения, от Дф — ф — фко для различных значений на. |
На величину контактной ( гальванической) коррозии могут оказывать влияние в дополнение к обычным факторам, влияющим на металл в отсутствие контакта, соотношение потенциалов металлов, находящихся в контакте, их поляризационные характеристики, относительная поверхность анода и катода, а также внутреннее и внешнее сопротивления гальванического тока.
В большинстве практических задач нагревания и охлаждения теплопроводность материала и коэффициент конвективной теплоотдачи имеют конечные значения, что и предопределяет необходимость рассмотрения и анализа влияния внутреннего и внешнего сопротивления на теплообмен.
|
Кривые распределения насыщенностей пласта в многорядной системе скважин на моменты времени ti, t3, t3, ( по В. С. Орлову. |
Выше принято, что по мере подхода фронта вытеснения к ряду скважин ряд отключается независимо от обводненности продукции его скважин. Для учета продолжающейся эксплуатации скважин в многорядных системах принимают, что зависимость насыщенности s от координаты х после прорыва воды в i — й ряд скважин имеет такой же параболический характер, как и до прорыва воды в первый ряд. Тогда расчеты выполняют аналогично, только внутренние и внешние сопротивления в водонефтяной зоне умножают на коэффициент aj, который определяют по насыщенно-стям zt ( на линиях рядов. Последние вычисляют в зависимости от суммарного количества жидкости, прошедшей через линию данного ряда.
Задача о диффузионном испарении капель, рассмотренная впервые Максвеллом, сегодня привлекает внимание исследователей. Все работы, касающиеся этого вопроса, можно разделить: а) по методам исследования — аналитическим и численным; б) по вкладу внутреннего и внешнего сопротивления процессам тепло — и массопереноса; в) на стационарные и нестационарные задачи; г) по отношению к внешней среде; д) по влиянию различных сил ( электрические, звуковые поля) на скорость испарения.
Что такое электродвижущая сила
Подробно этот вопрос мы рассмотрели в отдельной статье: https://samelectrik.ru/chto-takoe-eds-obyasnenie-prostymi-slovami.html
Под ЭДС понимается физическая величина, характеризующая работу каких-либо сторонних сил, находящихся в источниках питания постоянного или переменного тока. При этом, если имеется замкнутый контур, то можно сказать, что ЭДС равна работе сил по перемещению положительного заряда к отрицательному по замкнутой цепи. Или простыми словами, ЭДС источника тока представляет работу, необходимую для перемещения единичного заряда между полюсами.
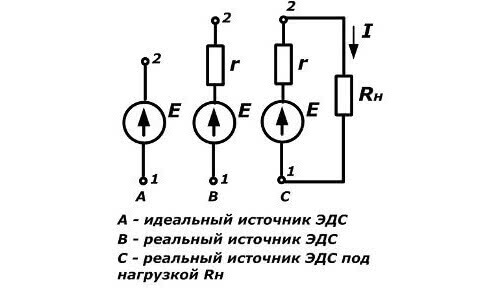
При этом если источник тока имеющего бесконечную мощность, а внутреннее сопротивление будет отсутствовать (позиция А на рисунке), то ЭДС можно рассчитать по закону Ома для участка цепи, т.к. напряжение и электродвижущая сила в этом случае равны.
I=U/R,
где U – напряжение, а в рассмотренном примере — ЭДС.
Однако, реальный источник питания имеет конечное внутреннее сопротивление. Поэтому такой расчет нельзя применять на практике. В этом случае для определения ЭДС пользуются формулой для полной цепи.
I=E/(R+r),
где E (также обозначается как «ԑ») — ЭДС; R – сопротивление нагрузки, r – внутреннее сопротивление источника электропитания, I – ток в цепи.
Однако, эта формула не учитывает сопротивление проводников цепи. При этом необходимо понимать, что внутри источника постоянного тока и во внешней цепи, ток течет в разных направлениях. Разница заключается в том, что внутри элемента он течет от минуса к плюсу, то во внешней цепи от плюса к минусу.
Это наглядно представлено на ниже приведенном рисунке:
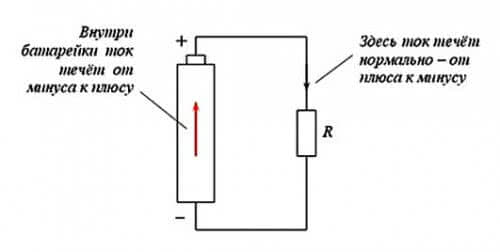
При этом электродвижущая сила измеряется вольтметром, в случае, когда нет нагрузки, т.е. источник питания работает в режиме холостого хода.
Чтобы найти ЭДС через напряжение и сопротивление нагрузки нужно найти внутреннее сопротивление источника питания, для этого измеряют напряжение дважды при разных токах нагрузки, после чего находят внутреннее сопротивление. Ниже приведен порядок вычисления по формулам, далее R1, R2 — сопротивление нагрузки для первого и второго измерения соответственно, остальные величины аналогично, U1, U2 – напряжения источника на его зажимах под нагрузкой.
Итак, нам известен ток, тогда он равен:
I1=E/(R1+r)
I2=E/(R2+r)
При этом:
R1=U1/I1
R2=U2/I2
Если подставить в первые уравнения, то:
I1=E/( (U1/I1)+r)
I2=E/( (U2/I2)+r)
Теперь разделим левые и правые части друг на друга:
(I1/I2)= [E/( (U1/I1)+r)]/[E/( (U2/I2)+r)]
После вычисления относительно сопротивления источника тока получим:
r=(U1-U2)/(I1-I2)
Внутреннее сопротивление r:
r= (U1+U2)/I,
где U1, U2 — напряжение на зажимах источника при разном токе нагрузки, I — ток в цепи.
Тогда ЭДС равно:
E=I*(R+r) или E=U1+I1*r
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. На рисунке приведена схема электрической цепи, состоящей из источника тока, ключа и двух параллельно соединённых резисторов. Для измерения напряжения на резисторе \( R_2 \) вольтметр можно включить между точками
1) только Б и В
2) только А и В
3) Б и Г или Б и В
4) А и Г или А и В
2. На рисунке представлена электрическая цепь, состоящая из источника тока, резистора и двух амперметров. Сила тока, показываемая амперметром А1, равна 0,5 А. Амперметр А2 покажет силу тока
1) меньше 0,5 А
2) больше 0,5 А
3) 0,5 А
4) 0 А
3. Ученик исследовал зависимость силы тока в электроплитке от приложенного напряжения и получил следующие данные.
Проанализировав полученные значения, он высказал предположения:
А. Закон Ома справедлив для первых трёх измерений.
Б. Закон Ома справедлив для последних трёх измерений.
Какая(-ие) из высказанных учеником гипотез верна(-ы)?
1) только А
2) только Б
3) и А, и Б
4) ни А, ни Б
4. На рисунке изображён график зависимости силы тока в проводнике от напряжения на его концах. Чему равно сопротивление проводника?
1) 0,25 Ом
2) 2 Ом
3) 4 Ом
4) 8 Ом
5. На диаграммах изображены значения силы тока и напряжения на концах двух проводников. Сравните сопротивления этих проводников.
1) \( R_1=R_2 \)
2) \( R_1=2R_2 \)
3) \( R_1=4R_2 \)
4) \( 4R_1=R_2 \)
6. На рисунке приведена столбчатая диаграмма. На ней представлены значения мощности тока для двух проводников (1) и (2) одинакового сопротивления. Сравните значения напряжения \( U_1 \) и \( U_2 \) на концах этих проводников.
1) \( U_2=\sqrt{3}U_1 \)
2) \( U_1=3U_2 \)
3) \( U_2=9U_1 \)
4) \( U_2=3U_1 \)
7. Необходимо экспериментально обнаружить зависимость электрического сопротивления круглого угольного стержня от его длины. Какую из указанных пар стержней можно использовать для этой цели?
1) А и Г
2) Б и В
3) Б и Г
4) В и Г
8. Два алюминиевых проводника одинаковой длины имеют разную площадь поперечного сечения: площадь поперечного сечения первого проводника 0,5 мм2, а второго проводника 4 мм2. Сопротивление какого из проводников больше и во сколько раз?
1) Сопротивление первого проводника в 64 раза больше, чем второго.
2) Сопротивление первого проводника в 8 раз больше, чем второго.
3) Сопротивление второго проводника в 64 раза больше, чем первого.
4) Сопротивление второго проводника в 8 раз больше, чем первого.
9. В течение 600 с через потребитель электрического тока проходит заряд 12 Кл. Чему равна сила тока в потребителе?
1) 0,02 А
2) 0,2 А
3) 5 А
4) 50 А
10. В таблице приведены результаты экспериментальных измерений площади поперечного сечения \( S \), длины \( L \) и электрического сопротивления \( R \) для трёх проводников, изготовленных из железа или никелина.
На основании проведённых измерений можно утверждать, что электрическое сопротивление проводника
1) зависит от материала проводника
2) не зависит от материала проводника
3) увеличивается при увеличении его длины
4) уменьшается при увеличении его площади поперечного сечения
11. Для изготовления резисторов использовался рулон нихромовой проволоки. Поочередно в цепь (см. рисунок) включали отрезки проволоки длиной 4 м, 8 м и 12 м. Для каждого случая измерялись напряжение и сила тока (см. таблицу).
Какой вывод можно сделать на основании проведённых исследований?
1) сопротивление проводника обратно пропорционально площади его поперечного сечения
2) сопротивление проводника прямо пропорционально его длине
3) сопротивление проводника зависит от силы тока в проводнике
4) сопротивление проводника зависит от напряжения на концах проводника
5) сила тока в проводнике обратно пропорциональна его сопротивлению
12. В справочнике физических свойств различных материалов представлена следующая таблица.
Используя данные таблицы, выберите из предложенного перечня два верных утверждения. Укажите их номера.
1) При равных размерах проводник из алюминия будет иметь меньшую массу и большее электрическое сопротивление по сравнению с проводником из меди.
2) Проводники из нихрома и латуни при одинаковых размерах будут иметь одинаковые электрические сопротивления.
3) Проводники из константана и никелина при одинаковых размерах будут иметь разные массы.
4) При замене никелиновой спирали электроплитки на нихромовую такого же размера электрическое сопротивление спирали уменьшится.
5) При равной площади поперечного сечения проводник из константана длиной 4 м будет иметь такое же электрическое сопротивление, что и проводник из никелина длиной 5 м.
Часть 2
13. Меняя электрическое напряжение на участке цепи, состоящем из никелинового проводника длиной 5 м, ученик полученные данные измерений силы тока и напряжения записал в таблицу. Чему равна площадь поперечного сечения проводника?
Польза повторения
Поскольку речь идет о мантре, закономерно возникает вопрос, как часто следует повторять этот священный звук. Выше мы говорили о трех составляющих ОМ-АУМ. Поэтому и повтор должен быть троекратным.
Исполняющий мантру неограничен в количестве повторений
Важно, чтобы это число делилось на три, а лучше – на девять. Таким образом, вы можете выбрать и 3 раза, и 9, и 27, и 54, и 108
Последнее число несет в себе особую силу, поэтому йоги ориентируются на 108 повторов. Неслучайно индуистские четки для медитации состоят из 108 бусин. Их называют джапа-мала – «гирлянда медитации».
При выполнении звуковой медитации помним о технике безопасности. Работа с мантрой ОМ-АУМ активирует мощные потоки энергии в теле. Поэтому начинаем с небольшого числа повторений, постепенно увеличивая их с каждым днем. В противном случае вы можете вызвать головокружение, повышение температуры тела и кровяного давления.
Иногда такие признаки возникают как реакция организма на выравнивание энергетики. В любом случае нагрузку желательно снизить. Кроме того, эти симптомы говорят о перенапряжении. Нужно предельно расслабиться и позволить энергии свободно течь по телу.
Медно-цинковый элемент
Принцип действия гальванических элементов интересно рассмотреть на примере медно-цинкового гальванического элемента, действие которого идет в счет энергии цинка и сульфата меди. В этом источнике пластина из меди помещена в раствор сульфата меди, а цинковый электрод погружен в раствор сульфата цинка. Растворы разделены пористой прокладкой во избежание смешивания, но обязательно соприкасаются.
Если цепь замкнута, поверхностный слой цинка окисляется. В процессе взаимодействия с жидкостью атомы цинка, превратившись в ионы, появляются в растворе. На электроде высвобождаются электроны, которые могут принимать участие в образовании тока.
Попадая на медный электрод, электроны принимают участие в восстановительной реакции. Из раствора на поверхностный слой поступают ионы меди, в процессе восстановления они превращаются в атомы меди, осаждаясь на медной пластине.
Суммируем происходящее: процесс работы гальванического элемента сопровождается переходом электронов восстановителя к окислителю по внешней части цепи. Реакции идут на обоих электродах. Внутри источника протекает ионный ток.
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.
- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
https://youtube.com/watch?v=f2rpF5ztAr0
Результат
Отлично!
Попытайтесь снова(
Выбор направления токов
Если при расчёте цепи направление токов неизвестны, то при составлении уравнений согласно законом Кирхгофа их необходимо предварительно выбрать произвольно и обозначить на схеме стрелками. В действительности направление токов в ветвях могут отличаться от произвольно выбранных. Поэтому выбранные направления токов называют положительными направлениями. Если в результате расчёта цепи какие-либо токи будут выражены отрицательными числами, то действительные направления этих токов обратны выбранным положительным направлениям.
Например
Рисунок 2
На рисунке 2,а представлен электрический узел. Произвольно, стрелками укажем направления токов (рисунок 2,б).
Важно! При выборе направления токов в ветвях, необходимо выполнения двух условий:1. Ток должен вытекать из узла через одну или несколько других ветвей;2. Хотя бы один ток должен входить в узел
Хотя бы один ток должен входить в узел.
Предположим, что после расчёта цепи получились следующие значения токов:
I1 = -5 А;
I2 = -2 A;
I3 = 3 А.
Так как значение тока I1 и I2 получились отрицательными, следовательно, действительно направление I1 и I2 противоположно ранее выбранным (рисунок 3).
Рисунок 3 — действительное направление токов обозначено синими стрелками
- I1 − I2 + I3 = 0;
- -5 − (-2) +3 = 0;
- -I1 + I2 + I3 = 0;
- -5 + 2 +3 = 0.
Сила тока и сопротивление
Как усилить поток воды из шланга? Можно добавить напор (увеличить давление), но не слишком сильно, иначе шланг разорвёт. А можно взять шланг большего диаметра.
То же справедливо и для проводника: чем больше он в сечении, тем больший поток электронов может пропустить. Но если сила тока окажется слишком большой, проводник перегреется и сгорит.
Именно так работают плавкие предохранители в электронных приборах: при резком скачке силы тока тонкий проводок перегорает, и устройство отключается от сети.

Плавкие предохранители: новый и отработанный
Чем короче и шире шланг, тем большее количество воды он способен пропустить за единицу времени. Также и с электричеством: сила тока, проходящего через проводник за секунду, зависит от сопротивления проводника. Только кроме длины и площади сечения на сопротивление влияет материал, из которого проводник сделан.
Формула сопротивления выглядит так:
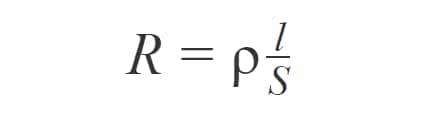
l — это длина проводника, S — площадь его сечения, а ρ — удельное сопротивление, у каждого материала оно своё.
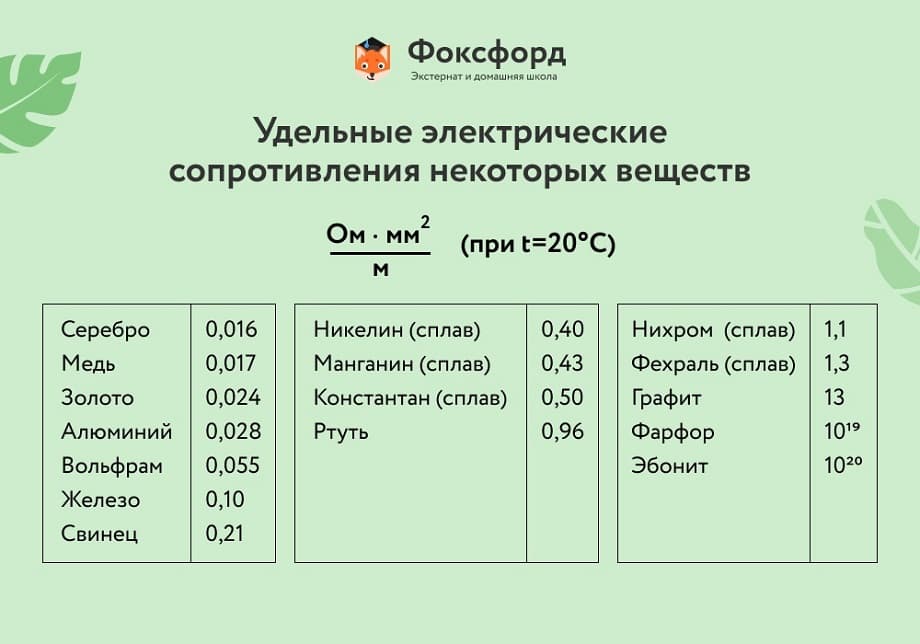
Вещества с низким удельным сопротивлением называются проводниками, они проводят электричество наиболее эффективно. Вещества с высоким удельным сопротивлением называют диэлектриками — их можно использовать в качестве изоляторов. Среднее положение занимают полупроводники — они проводят электричество, но не так хорошо, как проводники.
Сопротивление измеряется в Омах. Проводник обладает сопротивлением в 1 Ом, если на его концах возникает напряжение в 1 Вольт при силе тока в 1 Ампер.
Учите физику вместе с домашней онлайн-школой «Фоксфорда»! По промокоду PHYSICS82020 вы получите бесплатный доступ к курсу физики 8 класса, в котором изучается сила тока!
Второй закон Кирхгофа.
Второй закон Кирхгофа: в контуре электрической цепи алгебраическая сумма эдс равна алгебраической сумме падений напряжения на всех сопротивлениях данного контура.
где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.
Применение второго закона Кирхгофа
Для контура ABСDE, изображенного на рисунке 4, стрелками указаны положительные направления токов (произвольно). Составим уравнение согласно второму закону Кирхгофа. Для этого произвольно зададимся направлением обхода контура по часовой или против часовой стрелки. В данном примере направление обхода контура выберем по часовой стрелке.
Рисунок 4
При составлении уравнений по второму закону Кирхгофа, ЭДС записывается со знаком “+”, если ее направление совпадает с направлением произвольно выбранного обхода контура. В противном случае ЭДС записывается со знаком “-”.
Падения напряжения записываются со знаком “+”, если направление тока в нем совпадает с направлением обхода.
Начнём с эдс E1, так как её направление совпадает с обходом контура — записываем её со знаком “+” перед знаком равно.
Контур ABСDE E1 =
E2 направленна против обхода контура записываем со знаком “-” перед знаком равно.
Контур ABСDE E1 − E2 =
Так как больше ЭДС в контуре ABСDЕ нет — левая часть уравнения готова.
В правой части уравнения указываются падения напряжения контура, так как направления токов I1 и I2 совпадает с обходом контура – записываем падения напряжения со знаком “+”.
Контур ABСDЕE E1 − E2 = I1*R1 + I2*R2
Направление тока I3 не совпадет с обходом контура:
Контур ABСDE E1 − E2 = I1*R1 + I2*R2 − I3*R3.
Уравнение для контура готово.
Законы Кирхгофа являются основой для расчета электрической цепи, вот несколько методов применяющие данные законы.
Особенности внутреннего сопротивления источника тока
У идеального источника тока бесконечное сопротивление, а для подлинных источников можно представить приближенный вариант. Эквивалентная электросхема – это сопротивление, подключенное к источнику параллельно, и внешнее сопротивление.
Токовый выход от источника тока распределяется так: частично ток течет через наиболее высокое внутреннее сопротивление и через низкое сопротивление нагрузки.
Выходной ток будет находиться из суммы токов на внутреннем сопротивлении и нагрузочного Iо = Iн + Iвн.
Получается:
Iн = Iо — Iвн = Iо — Uн/r.
Эта зависимость показывает, что когда внутреннее сопротивление источника тока растет, тем больше снижается ток на нем, а резистор нагрузки получает большую часть тока. Интересно, что напряжение влиять не будет на токовую величину.
Выходное напряжение реального источника:
Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:
- Автомобильный свинцово-кислотный аккумулятор напряжением 12 вольт и ёмкостью 55 А·ч
- Восемь батареек типоразмера АА, соединенных последовательно. Суммарное напряжение такой батареи также 12 вольт, ёмкость значительно меньше — примерно 1 А·ч
Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).
Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем
сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что ипросто «сопротивление».
Что такое напряжение?
Существует разница в электрических состояниях на полюсах (клеммах) источника. На отрицательном полюсе имеется избыток электронов и нехватка электронов на положительном. В замкнутой цепи тока электроны движутся от отрицательной половины к положительной половине через проводники и приборы. Разность электрических потенциалов называется электрическим напряжением . Электрическое напряжение равно количеству работ, выполняемых электрической силой при перемещении заряда из одной точки поля в другую и этой зарядке. Электрическое напряжение измеряется вольтах . Измеритель напряжения называется вольтметром.
Нахождение внутреннего сопротивления[править]
Расчётправить
Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).
Пусть, имеется двухполюсник, который может быть описан приведенной выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:
- ЭДС генератора напряжения U
- Внутреннее сопротивление r
В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:
| \( \begin{matrix} U_{out1} = U – r I_1 \\ U_{out2} = U – r I_2 \end{matrix} \) |
(1) |
где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:
| \( r = \frac {U_{out1} – U_{out2}} {I_2 – I_1}, \quad U = U_{out1} + I_1 \frac {U_{out1} – U_{out2}} {I_2 – I_1} = U_{out1} + I_1 r \) |
Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (1) записывается следующим образом:
| \( \begin{matrix} U_{oc} = U – 0 \\ 0 = U – r I_{sc} \end{matrix} \) |
где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:
| \( r = \frac {U_{oc}} {I_{sc}}, \quad U = U_{oc} \) |
(2) |
Таким образом, чтобы расчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:
- Расчитать выходное напряжение двухполюсника в режиме холостого хода
- Расчитать выходной ток двухполюсника в режиме короткого замыкания
- На основании полученных значений найти r и U по формуле (2).
Измерениеправить
Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчета — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощенной формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.
Часто применяется следующий простой способ измерения, не требующий вычислений:
- Измеряется напряжение холостого хода
- В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нем составило половину от напряжения холостого хода.
После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.
Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.
Реактивное внутреннее сопротивлениеправить
Если эквивалентная схема двухполюсника содержит реактивные элементы – конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.
Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:
- Можно искать различные параметры комплексного значения: модуль, , только или часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
- Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.
Разбираемся что такое ток и сопротивление
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.
Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.
Примерно так можно себе представить электрический ток
Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.
Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.
Цепь для проверки зависимости силы тока от сопротивления
Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.
Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.