Конспект "закон ома. соединение проводников"

Аналогия с электрическим сопротивлением проводника на примере резистора

Чтобы суметь рассчитать импеданс цепи, нужно представлять, как себя ведут различные входящие в нее элементы: катушки индуктивности, резисторные и емкостные детали, с точки зрения вклада в составляющие общей резистивности цепи.

Активное сопротивление

Резистор относится к числу пассивных деталей цепи, не содержащих внутренних источников электроэнергии, при этом почти все создаваемое им противодействие приходится на активную компоненту. Реактивная составляющая если и присутствует, то настолько мала, что ею зачастую принято пренебрегать. Это связано с тем, что отношение напряжения на деталь и электротока, проходящего через нее, не зависит от их частоты. Когда к резисторной детали присоединяют источник напряжения (обозначим его U), через нее будет идти электроток значением I. Если к концам радиодетали подсоединяют источник тока, равного I, между ними будет иметь место падение напряжения U.

Резисторы – источники активного сопротивления

Реактивное сопротивление

К основным компонентам электроцепей, несущим такую нагрузку, относятся дроссели (и подобные им индуктивные элементы) и конденсаторы. При достижении резонанса наблюдается наименьшее значение общего противодействия подключенных последовательно конденсатора и дросселя и наибольшее – включенных параллельно.

Индуктивная нагрузка

Если индуктивный дроссель подключить к постоянному току, на нем будут наблюдаться следующие эффекты: резистивность будет приближаться к нулевому значению, а при пропускании электротока через катушечный элемент падение напряжения будет отсутствовать, независимо от токовой величины:

R=U/I=0/I=0.

Такие цифры справедливы для идеального дросселя, на практике они все же несколько отклоняются от нуля. Если к детали будет приложен переменный ток, напряжение между катушечными выводами будет отличным от нуля.

Катушка индуктивности

Емкостная нагрузка

При включении идеального конденсаторного элемента в сеть с постоянным напряжением его резистивность будет иметь очень большую величину, стремящуюся к бесконечной. Когда к радиодетали прикладывают такое напряжение, проходящий через нее ток будет равен нулю. Если к выводам конденсатора подсоединить источник переменного напряжения, ток будет ненулевым.

Детали, обладающие емкостью

Данные эффекты, наблюдаемые на емкостных радиодеталях и катушках, нельзя описывать в категориях активного противодействия в условиях константного электротока, так как последнее подразумевает стабильное, независимое от условий и не изменяющееся во времени отношение электротока и напряжения и исключает явление сдвига фаз между этими величинами. Таким образом, становится целесообразным введение для реактивных деталей характеристики, связывающей электроток и напряжение так, как это делает активное противодействие в омовском законе для константного тока.

Важно! При рассмотрении поведения катушек и конденсаторов под действием гармонических сигналов обнаруживается, что токовая сила и напряжение могут быть связаны константной величиной, которую также называют импедансом. При ее изучении применяется понятие о гармонических сигналах, учитывающее как их амплитудные характеристики, так и особенности, связанные с фазами. Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока

В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой

Такое значение импеданса можно определить как частное комплексной амплитуды, которой обладает напряжение приложенного к двухполюсному элементу сигнала, и комплексной амплитуды идущего через элемент электротока. В отношении пассивных электроцепей со стабильными показателями в устоявшемся режиме стоит сказать, что импедансный показатель у них не будет привязанным к течению времени. Если временной параметр при формульной записи не сокращается, то категория импеданса для рассматриваемого двухполюсника окажется неприменимой.

Электрические цепи. Последовательное и параллельное соединения проводников

Подробности: Просмотров: 346

«Физика – 10 класс»

Как выглядит зависимость силы тока в проводнике от напряжения на нём?
Как выглядит зависимость силы тока в проводнике от его сопротивления?

От источника тока энергия может быть передана по проводам к устройствам, потребляющим энергию: электрической лампе, радиоприёмнику и др. Для этого составляют электрические цепи различной сложности.

К наиболее простым и часто встречающимся соединениям проводников относятся последовательное и параллельное соединения.

Последовательное соединение проводников.

При последовательном соединении электрическая цепь не имеет разветвлений. Все проводники включают в цепь поочерёдно друг за другом. На рисунке (15.5, а) показано последовательное соединение двух проводников 1 и 2, имеющих сопротивления R₁ и R₂. Это могут быть две лампы, две обмотки электродвигателя и др.

Сила тока в обоих проводниках одинакова, т. е.

I₁ = I₂ = I. (15.5)

В проводниках электрический заряд в случае постоянного тока не накапливается, и через любое поперечное сечение проводника за определённое время проходит один и тот же заряд.

Напряжение на концах рассматриваемого участка цепи складывается из напряжений на первом и втором проводниках:

U = U₁ + U₂.

Применяя закон Ома для всего участка в целом и для участков с сопротивлениями проводников R1 и R2, можно доказать, что полное сопротивление всего участка цепи при последовательном соединении равно:

R = R₁ + R₂. (15.6)

Это правило можно применить для любого числа последовательно соединённых проводников.

Напряжения на проводниках и их сопротивления при последовательном соединении связаны соотношением

Параллельное соединение проводников.

На рисунке (15.5, б) показано параллельное соединение двух проводников 1 и 2 сопротивлениями R₁ и R₂. В этом случае электрический ток I разветвляется на две части. Силу тока в первом и втором проводниках обозначим через I₁ и I₂.

Так как в точке а — разветвлении проводников (такую точку называют узлом) — электрический заряд не накапливается, то заряд, поступающий в единицу времени в узел, равен заряду, уходящему из узла за это же время. Следовательно,

I = I₁ + I₂. (15.8)

Напряжение U на концах проводников, соединённых параллельно, одинаково, так как они присоединены к одним и тем же точкам цепи.

В осветительной сети обычно поддерживается напряжение 220 В. На это напряжение рассчитаны приборы, потребляющие электрическую энергию. Поэтому параллельное соединение — самый распространённый способ соединения различных потребителей. В этом случае выход из строя одного прибора не отражается на работе остальных, тогда как при последовательном соединении выход из строя одного прибора размыкает цепь. Применяя закон Ома для всего участка в целом и для участков проводников сопротивлениями R₁ и R₂, можно доказать, что величина, обратная полному сопротивлению участка ab, равна сумме величин, обратных сопротивлениям отдельных проводников:

Отсюда следует, что для двух проводников

Напряжения на параллельно соединённых проводниках равны: I₁R₁ = I₂R₂. Следовательно,

Обратим внимание на то, что если в какой-то из участков цепи, по которой идёт постоянный ток, параллельно к одному из резисторов подключить конденсатор, то ток через конденсатор не будет идти, цепь на участке с конденсатором будет разомкнута. Однако между обкладками конденсатора будет напряжение, равное напряжению на резисторе, и на обкладках накопится заряд q = CU

Рассмотрим цепочку сопротивлений R — 2R, называемую матрицей (рис. 15.6).

На последнем (правом) звене матрицы напряжение делится пополам из-за равенства сопротивлений, на предыдущем звене напряжение тоже делится пополам, поскольку оно распределяется между резистором сопротивлением R и двумя параллельными резисторами сопротивлениями 2R и т. д. Эта идея — деления напряжения — лежит в основе преобразования двоичного кода в постоянное напряжение, что необходимо для работы компьютеров.

Следующая страница «Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников»»

Назад в раздел «Физика – 10 класс, учебник Мякишев, Буховцев, Сотский»

Законы постоянного тока – Физика, учебник для 10 класса – Класс!ная физика

Электрический ток. Сила тока —
Закон Ома для участка цепи. Сопротивление —
Электрические цепи. Последовательное и параллельное соединения проводников —
Примеры решения задач по теме «Закон Ома. Последовательное и параллельное соединения проводников» —
Работа и мощность постоянного тока —
Электродвижущая сила —
Закон Ома для полной цепи —
Примеры решения задач по теме «Работа и мощность постоянного тока. Закон Ома для полной цепи»

Понятие тока и напряжения

Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.

В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.

Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.

Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.

Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.

При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.

https://youtube.com/watch?v=YXD4ThltnQo

§ 2.9. Закон Ома для электрической цепи переменного тока

Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С (рис. 2.20).

Рис. 2.20

Чему равна амплитуда силы тока в такой цепи (колебательном контуре), если на ее концах поддерживается напряжение u(t) = U sin ωt?

Мы видели, что при включении по отдельности в цепь проводника с активным сопротивлением R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами (2.6.2), (2.7.3) и (2.8.4). Амплитуды же напряжений на резисторе, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так:

В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи переменного тока, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах.

Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.

Действительно, квазистационарный ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлением. Однако только на участке с активным сопротивлением колебания напряжения и силы тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний силы тока на π/2 (см. § 2.7), а на катушке индуктивности колебания напряжения опережают колебания силы тока на π/2 (см. § 2.8).

Векторная диаграмма электрической цепи

Для вывода закона Ома в случае электрической цепи переменного тока, изображенной на рисунке 2.20, нужно уметь складывать мгновенные колебания напряжений, сдвинутых по фазе друг относительно друга. Проще всего выполнять сложение нескольких гармонических колебаний с помощью векторных диаграмм, о которых было рассказано в § 1.11. Векторная диаграмма электрических колебаний в цепи позволит нам определить амплитуду силы тока в зависимости от амплитуды напряжения и сдвиг фаз между силой тока и напряжением.

Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока _m. Этот вектор изобразим в виде вертикальной стрелки (рис. 2.21). Напряжение на резисторе совпадает по фазе с силой тока. Поэтому вектор _mR должен совпадать по направлению с вектором _m. Его модуль равен U_mR = I_mR.

Рис. 2.21

Колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2 и соответствующий вектор и _mL должен быть повернут относительно вектора _m на π/2. Его модуль равен U_mL = IωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор _mL следует повернуть налево на π/2. (Можно было бы, конечно, поступить и наоборот.)

Вектор напряжения на конденсаторе _mC отстает по фазе от вектора _m на π/2 и поэтому повернут на этот угол относительно вектора _m направо. Его модуль равен .

Для нахождения вектора суммарного напряжения _m нужно сложить три вектора: _mR, _mL и _mC. Вначале удобнее сложить два вектора _mL и _mC (рис. 2.22).

Рис. 2.22

Модуль этой суммы равен , если . Именно такой случай изображен на рисунке. После этого, сложив вектор _mL + _mC с вектором _mR, получим вектор _m, характеризующий колебания напряжения в сети.

По теореме Пифагора (из треугольника АОВ):

или

Из равенства (2.9.2) можно найти амплитуду силы тока в цепи:

Это и есть закон Ома для электрической цепи переменного тока, изображенной на рисунке 2.20.

Благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи (см. рис. 2.20) выражается так:

От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин. Они связаны друг с другом точно так же, как и амплитуды в формуле (2.9.3):

Мгновенное значение силы тока меняется со временем гармонически:

где φ_c, — разность фаз между силой тока и напряжением в сети. Она зависит от частоты со и параметров цепи R, L, С.

Сдвиг фаз между током и напряжением

Сдвиг фаз φ_c, между колебаниями силы тока и напряжения равен по модулю углу φ между векторами _m и _m (см. рис. 2.22). Как следует из этого рисунка,

Согласно рисунку 2.22, сила тока отстает от напряжения по фазе при условии . Поэтому сдвиг фаз φ_c = -φ и

В частных случаях цепей с активным, емкостным и индуктивным сопротивлениями из этой формулы получаются правильные значения сдвига фаз.

Формула сопротивления при параллельном и последовательном соединении

Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением.

В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным.

Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.

Последовательное соединение проводников

В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.

Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.

Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:

Сила тока на всех участках цепи будет одинаковой.
Общее напряжение цепи составляет сумму напряжений на каждом участке.
Общее сопротивление включает в себя сопротивления каждого отдельного проводника.

Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.

Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R – общее сопротивление, R1 – сопротивление одного элемента, а n – количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.

Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является елочная гирлянда, когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.

Параллельное соединение проводников

В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.

Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный амперметр. Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.

После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 – силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.

Закон Ома для участка цепи

Для описания электрической цепи не содержащего ЭДС можно использовать закон Ома для участка цепи. Это наиболее простая форма записи. Он выглядит так:

I=U/R

Где I – это ток, измеряется в Амперах, U – напряжение в вольтах, R – сопротивление в Омах.

Такая формула нам говорит, что ток прямопропорционален напряжению и обратнопропорционален сопротивлению – это точная формулировка Закона Ома. Физический смысл этой формулы – это описать зависимость тока через участок цепи при известном его сопротивлении и напряжении.

Внимание! Эта формула справедлива для постоянного тока, для переменного тока она имеет небольшие отличия, к этому вернемся позже. Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:. Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:

Кроме соотношения электрических величин данная форма нам говорит о том, что график зависимости тока от напряжения в сопротивлении линеен и выполняется уравнение функции:

f(x) = ky или f(u) = IR или f(u)=(1/R)*I

Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы или для определения тока через него при известном напряжении и сопротивлении. Например, у нас есть резистор R сопротивлением в 6 Ом, к его выводам приложено напряжение 12 В. Необходимо узнать, какой ток будет протекать через него. Рассчитаем:

I=12 В/6 Ом=2 А

Идеальный проводник не имеет сопротивления, однако из-за структуры молекул вещества, из которого он состоит, любое проводящее тело обладает сопротивлением. Например, это стало причиной перехода с алюминиевых проводов на медные в домашних электросетях. Удельное сопротивление меди (Ом на 1 метр длины) меньше чем алюминия. Соответственно медные провода меньше греются, выдерживают большие токи, значит можно использовать провод меньшего сечения.

Еще один пример — спирали нагревательных приборов и резисторов обладают большим удельным сопротивлением, т.к. изготавливаются из разных высокоомных металлов, типа нихрома, кантала и пр. Когда носители заряда движутся через проводник, они сталкиваются с частицами в кристаллической решетке, вследствие этого выделяется энергия в виде тепла и проводник нагревается. Чем больше ток – тем больше столкновений – тем больше нагрев.

Чтобы снизить нагрев проводник нужно либо укоротить, либо увеличить его толщину (площадь поперечного сечения). Эту информацию можно записать в виде формулы:

R_провод=ρ(L/S)

Где ρ – удельное сопротивление в Ом*мм2/м, L – длина в м, S – площадь поперечного сечения.

Что такое общее сопротивление цепи

Если говорить простыми словами, общее сопротивление электрической цепи – это такое R, которое она оказывает на напряжение в ее проводниках и приборах. Существует два типа напряжения (исходя из силы тока) – постоянное и переменное. Так же и сопротивление делится на активное и реактивное, которое, в свою очередь, подразделяется на индуктивное и емкостное. Активный тип не зависит от частот сети

Также для него абсолютно не важно, какой ток протекает по проводникам. Реактивный же, наоборот, зависит от частоты, причем емкостная характеристика в конденсаторах и индуктивная в трансформаторах ведут себя по-разному

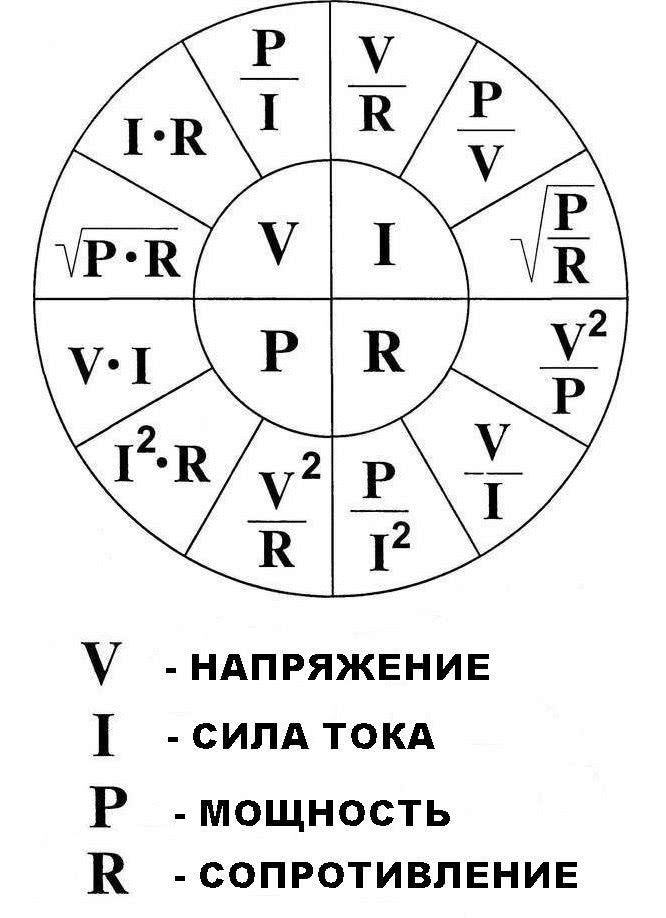
Закон Ома

Помимо сопротивления подключенных в сеть электроприборов, на общее состояние оказывают влияние даже промежуточные провода, также имеющие сопротивляемость напряжению.

Резистор – основной элемент сопротивляемости цепи

Как правильно рассчитать сопротивление

Применяется закон Ома для участка цепи – расчет сопротивления делается по формуле R = U/I, где

U – падение напряжение на конкретном резистивном элементе;
I – ток, протекающий через него.

Для двух элементов считаем Rобщ = R1+R2.

Для нескольких сопротивлений разного номинала Rобщ = R1+R2+R3+…+Rn.

При параллельном соединении

Расчет для двух резисторов делаем по формуле Rобщ = (R1×R2)/(R1+R2).

Сопротивление параллельных резисторов с разным номиналом рассчитываем по формуле

Rобщ = 1/(1/R1+1/R2+1/R3+…+1/Rn).

Для элементов, соединенных в параллель, суммарное сопротивление всегда ниже наименьшего номинального.

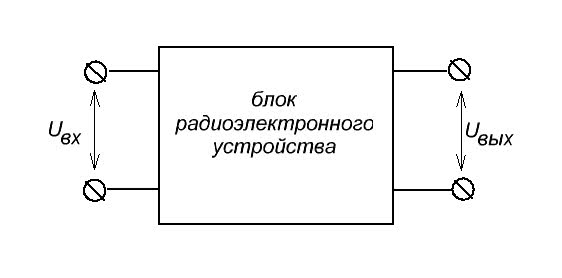
Входное сопротивление

Итак, имеем какой-либо блок. Как принято во всем мире, слева – это вход блока, справа – выход.

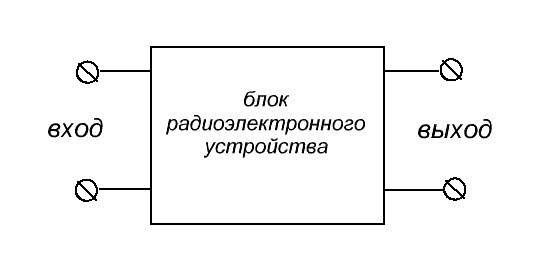
Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение U_вхот другого блока или от источника питания, а на его выходе появится напряжение U_вых(или не появится, если блок является конечным).

Но раз уж мы подаем напряжение на вход (входное напряжение U_вх), следовательно, у нас этот блок будет кушать какую-то силу тока I_вх.

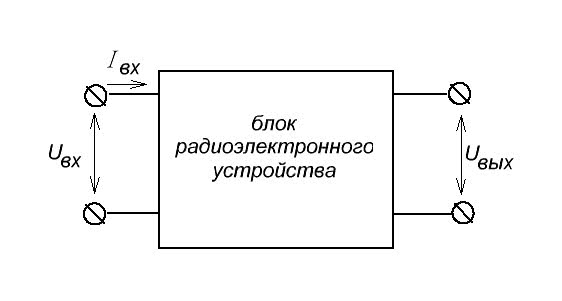
Теперь самое интересное… От чего зависит I_вх? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.

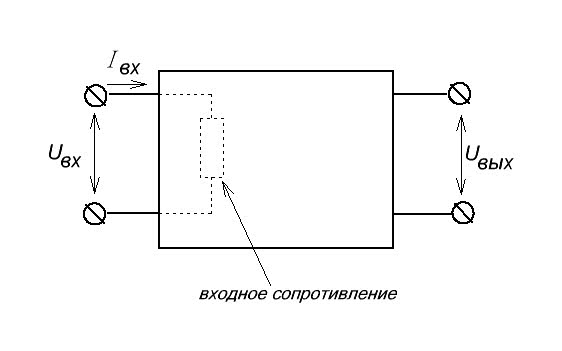
То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.

Как подключить резистор в цепь

Для сборки составного устройства необходимо соединить несколько элементов одним из основных методов и таким образом получить нужный номинальный показатель. В практике это используется очень часто. Навыки правильного подключения устройств и расчета их общего сопротивления используются мастерами для ремонта проводки или радиолюбителями при сборке устройства. В интернете можно найти много схем с различным видом подключения. Ниже описано какое соединение резисторов называется параллельным.

Параллельное соединение резисторов схема

Параллельно

Параллельное — это одно из двух типов электрических соединений, когда два вывода единственного устройства соединены с соответствующими выводами других элементов. Очень часто их могут соединять последовательно или параллельно, чтобы сделать более усложненные электрические схемы.

При этом виде соединения напряжение на всех устройствах будет равным, а проходящий через них ток — пропорционален их сопротивлению.

Такой вариант подключения один из простых, очень часто именно его рекомендуют использовать тем, кто не имеет опыта работы с электрикой.

Последовательно

Формула расчета достаточно легкая. Общее сопротивление при параллельном соединении формула:

Rобщ. = R1+R2+R3+…+Rn.

Сопротивление двух и более параллельно соединенных резисторов указано как Rобщ.

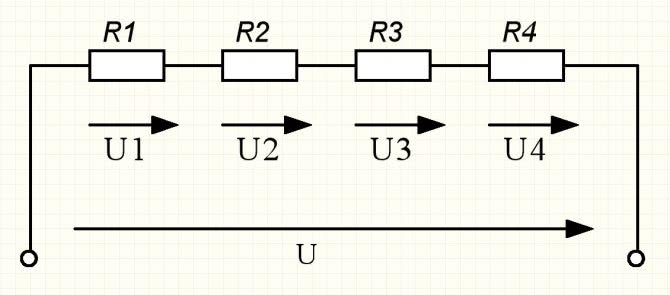
Последовательный способ подключения

Остальные элементы указываются как R, R2, R3 и так далее.

Вам это будет интересно Особенности профессии электрика

Обратите внимание! Используя последовательное соединение, необходимо запомнить один важный нюанс. Из общего количества компонентов, соединённых последовательным методом, основную роль занимает тот, у которого самое высокое сопротивление

Как это понять? Для примера, если необходимо соединить три устройства, номинал которых будет равняться 1, 10 и 100 Ом, то в итоге получится составной на 111 Ом.

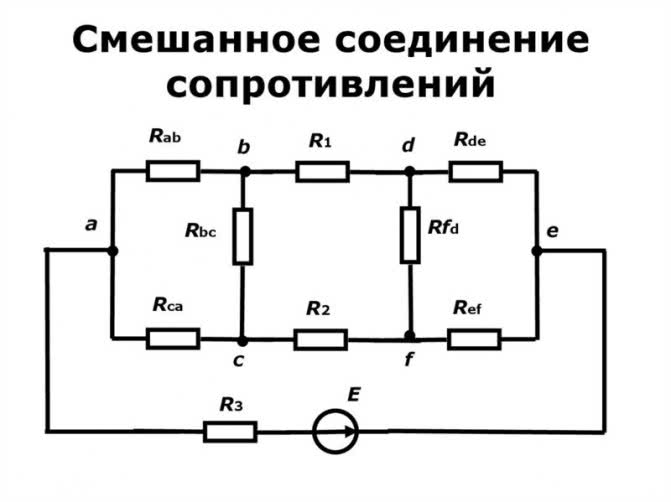
Смешанный тип подключения

Если исключить прибор на 100 Ом, то все сопротивление схемы резко снизится до 11 Ом. А если исключить, например, на 1 Ом, то показатель получится уже 110 Ом. В итоге устройства с небольшим сопротивлениями в последовательной цепочке почти не влияют на все показатели.

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Пример №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

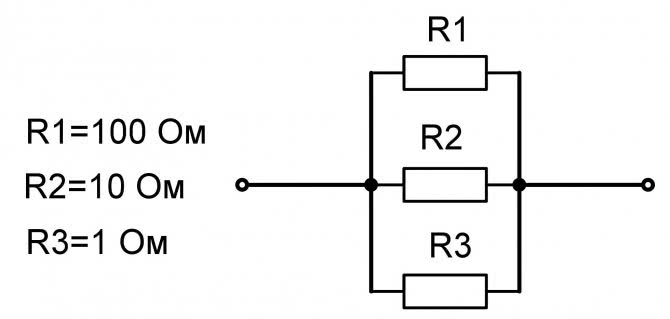
Пример расчета №2

Найти общее сопротивление R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи можно определить как:
I = I1 + I2
Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
Таким образом, общий ток будет равен:
I = 0,545 мА + 0,255 мА = 0,8 мА
Это также можно проверить, используя закон Ома:
I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора входящего в параллельное соединение.

Последовательное и параллельное соединения проводников