Что такое сопротивление

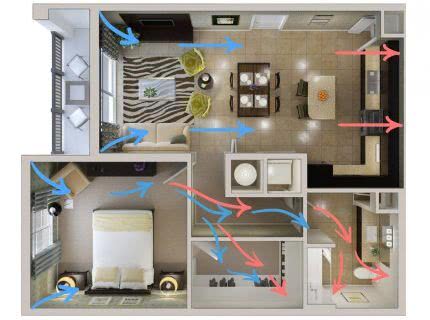
Параллельное и последовательное соединение

Все это время речь шла о цепях с одним резистором. Рассмотрим, что происходит, если их больше.

Решим несколько задач на последовательное и параллельное соединение.

Задачка раз

Найти общее сопротивление цепи.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом, R4 = 4 Ом.

Решение:

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + R2 + R3 + R4 = 1 + 2 + 3 + 4 = 10 Ом

Ответ: общее сопротивление цепи равно 10 Ом

Задачка два

Найти общее сопротивление цепи.

R1 = 4 Ом, R2 = 2 Ом

Решение:

Общее сопротивление при параллельном соединении рассчитывается по формуле:

R = (R1 * R2)/R1 + R2 = 4*2/4+2 = 4/3 = 1 ⅓ Ом

Ответ: общее сопротивление цепи равно 1 ⅓ Ом

Задачка три

Найти общее сопротивление цепи, состоящей из резистора и двух ламп.

R1 = 1 Ом, R2 = 2 Ом, R3 = 3 Ом

Решение:

Сначала обозначим, что лампы с точки зрения элемента электрической цепи не отличаются от резисторов. То есть у них тоже есть сопротивление, и они также влияют на цепь.

В данном случае соединение является смешанным. Лампы соеденены параллельно, а последовательно к ним подключен резистор.

Сначала посчитаем общее сопротивление для ламп. Общее сопротивление при параллельном соединении рассчитывается по формуле:

Rламп = (R2 * R3)/R2 + R3 = 2*3/2+3 = 6/5 = 1,2 Ом

Общее сопротивление при последовательном соединении рассчитывается по формуле:

R = R1 + Rламп = 1 + 1,2 = 2,2 Ом

Ответ: общее сопротивление цепи равно 2,2 Ом.

Наконец-то, последняя и самая сложная задача! В ней собрали все самое серьезное из этой статьи .

Задачка четыре со звездочкой

К аккумулятору с ЭДС 12 В, подключена лампочка и два параллельно соединенных резистора сопротивлением каждый по 10 Ом. Известно, что ток в цепи 0,5 А, а сопротивление лампочки R/2. Найти внутреннее сопротивление аккумулятора.

Решение:

Найдем сначала сопротивление лампы.

Rлампы = R/2 = 10/2 = 5 Ом

Теперь найдем общее сопротивление двух параллельно соединенных резисторов.

Rрезисторов = (R * R)/R + R = R^2)/2R = R/2 = 10/2 = 5 Ом

И общее сопротивление цепи равно:

R = Rлампы + Rрезисторов = 5 + 5 = 10 Ом

Выразим внутреннее сопротивление источника из закона Ома для полной цепи.

I = ε/(R + r)

R + r = ε/I

r = ε/I — R

Подставим значения:

r = 12/0,5 — 10 = 14 Ом

Ответ: внутреннее сопротивление источника равно 14 Ом.

Цветовая

Буквенные и цифровые символы сошли на нет, современная маркировка сопротивления является цветной. А, точнее, состоит она из цветных полосок, которые нанесены по окружности корпуса элемента. Таких полосок может быть от трех до шести.

Именно такое обозначение было создано для того, чтобы легче можно было бы считывать номинальные параметры резистора в независимости от места его установки и положения. Хотя надо сказать о том, что огромное разнообразие цветовой маркировки создает трудности в запоминании цвета оформления. Поэтому в интернете есть много онлайн калькуляторов, с помощью которых можно легко определить характеристики резисторов. В них надо просто вставлять цвета, обозначенные полосками. В результате калькулятор выдаст параметр элемента.

Обозначение резисторов на принципиальных схемах.

На принципиальных схемах постоянные резисторы, независимо от их типа, изображают в виде прямоугольника, а выводы резистора изображают в виде линий, проведенных от боковых сторон прямоугольника. Такое обозначение принято повсеместно, однако в некоторых зарубежных схемах используется обозначение резистора в форме зубчатой линии (пилы).

Рядом с условным обозначением ставят латинскую букву «R» и порядковый номер резистора в схеме, а также указывают его номинальное сопротивление в единицах измерения Ом, кОм, МОм.

Значение сопротивления от 0 до 999 Ом обозначают в омах, но единицу измерения не ставят:

15 — 15 Ом680 – 680 Ом920 — 920 Ом

На некоторых зарубежных схемах для обозначения Ом ставят букву R:

1R3 — 1,3 Ом33R – 33 Ом470R — 470 Ом

Значение сопротивления от 1 до 999 кОм обозначают в килоомах с добавлением буквы «к»:

1,2к — 1,2 кОм10к — 10 кОм560к — 560 кОм

Значение сопротивления от 1000 кОм и больше обозначают в единицах мегаом с добавлением буквы «М»:

1М — 1 МОм3,3М — 3,3 МОм56М — 56 МОм

Резистор применяют согласно мощности, на которую он рассчитан, и которую может выдержать без риска быть испорченным при прохождении через него электрического тока. Поэтому на схемах внутри прямоугольника прописывают условные обозначения, указывающие мощность резистора: двойной косой чертой обозначают мощность 0,125 Вт; прямой чертой, расположенной вдоль значка резистора, обозначают мощность 0,5 Вт; римскими цифрами обозначается мощность от 1 Вт и выше.

Сопротивление проводника

Так почему бы все эти свойства не применить также к проводнику? Чем тоньше и длиннее проводник, тем больше его сопротивление электрическому току. Большую роль играет также материал, из которого он изготовлен.

Поэтому, окончательная формула будет принимать вид

формула сопротивления проводника

В технике до сих пор применяется устаревшая единица измерения удельного сопротивления Ом × мм2 /м.  Чтобы перевести  в Ом × м, достаточно умножить на 10-6, так как 1 мм2=10-6 м2.

удельное сопротивление веществ

Как вы видите из таблицы выше, самым маленьким удельным сопротивлением обладает серебро, поэтому провод из серебра будет наилучшим проводником. Ну а самым распространенными и дешевыми проводниками являются медь и алюминий. Именно эти два металла в основном используются во всей электронной и электротехнической промышленности.

Вещества, которые оказывают наименьшее сопротивление электрическому току и обладают очень малым сопротивлением называются проводниками, а вещества, которые обладают ну очень большим сопротивлением электрическому току и почти его не пропускают через себя, называются диэлектриками. Между ними стоит класс .

Отдельный участок и полная электрическая цепь

Закон Ома, применительно к участку или всей цепи, может рассматриваться в двух вариантах расчетов:

• Отдельный краткий участок. Является частью схемы без источника ЭДС.
• Полная цепь, состоящая из одного или нескольких участков. Сюда же входит источник ЭДС со своим внутренним сопротивлением.

Расчет тока участка электрической схемы

В этом случае применяется основная формула I = U/R, в которой I является силой тока, U – напряжением, R – сопротивлением. По ней можно сформулировать общепринятую трактовку закона Ома:

Данная формулировка является основой для многих других формул, представленных на так называемой «ромашке» в графическом исполнении. В секторе Р – определяется мощность, в секторах I, U и R – проводятся действия, связанные с силой тока, напряжением и сопротивлением.

Каждое выражение – и основное и дополнительные, позволяют рассчитать точные параметры элементов, предназначенных для использования в схеме.

Специалисты, работающие с электрическими цепями, выполняют быстрое определение любого из параметров по методике треугольников, изображенных на рисунке.

В расчетах следует учитывать сопротивление проводников, соединяющих между собой элементы участка. Поскольку они изготавливаются из разных материалов, данный параметр будет отличаться в каждом случае. Если же потребуется сформировать полную схему, то основная формула дополняется параметрами источника напряжения, например, аккумуляторной батареи.

Вариант расчета для полной цепи

Полная цепь состоит из отдельно взятых участков, объединенных в единое целое вместе с источником напряжения (ЭДС). Таким образом, существующее сопротивление участков дополняется внутренним сопротивлением подключенного источника. Следовательно, основная трактовка, рассмотренная ранее, будет читаться следующим образом: I = U / (R + r). Здесь уже добавлен резистивный показатель (r) источника ЭДС.

С точки зрения чистой физики этот показатель считается очень малой величиной. Однако, на практике, рассчитывая сложные схемы и цепи, специалисты вынуждены его учитывать, поскольку дополнительное сопротивление оказывает влияние на точность работы. Кроме того, структура каждого источника очень разнородная, в результате, сопротивление в отдельных случаях может выражаться достаточно высокими показателями.

Приведенные расчеты выполняются применительно к цепям постоянного тока. Действия и расчеты с переменным током производятся уже по другой схеме.

Действие закона к переменной величине

При переменном токе сопротивление цепи будет представлять из себя так называемый импеданс, состоящий из активного сопротивления и реактивной резистивной нагрузки. Это объясняется наличием элементов с индуктивными свойствами и синусоидальной величиной тока. Напряжение также является переменной величиной, действующей по своим коммутационным законам.

Следовательно, схема цепи переменного тока по закону Ома рассчитывается с учетом специфических эффектов: опережения или отставания величины тока от напряжения, а также наличия активной и реактивной мощности. В свою очередь, реактивное сопротивление включает в себя индуктивную или емкостную составляющие.

Все этим явлениям будет соответствовать формула Z = U / I или Z = R + J * (XL – XC), в которой Z является импедансом; R – активной нагрузкой; XL , XC – индуктивной и емкостной нагрузками; J – поправочный коэффициент.

Единица измерения сопротивления в системе СГС

В системе СГС (сантиметр, грамм, секунда) единица сопротивления не имеет названия, вернее она называется единица сопротивления СГС, обозначается как $ед.{СГС}_R$. Единица электрического сопротивления в СГС ($1\ ед.{СГС}_R$) равна сопротивлению участка цепи, при котором постоянный ток силой 1 единица СГС тока (1 $ед.\ {СГС}_I$), вызывает падение напряжения 1 СГС напряжения (1$\ ед.\ {СГС}_U$). При этом:

Между омом и единицей сопротивления в СГС следующее соотношения:

В расширениях к системе СГС единицы сопротивление называют: статом. Статом — единица измерения сопротивления в системе СГСЭ и системе Гаусса. Это сопротивление проводника у которого при напряжении на концах в один статвольт течет ток один статампер. Обозначают статом как $1stat{\mathbf \Omega }$\textbf{.}\textit{}

В другом расширении системы СГС, СГСМ сопротивление измеряют в абомах($ab{\mathbf \Omega }$). Абом соотносится с омом как:

В системе СГСМ выполняется равенство:

где $abV$ — абвольт; $abA$ — абампер.

Определение омического сопротивления электрическому току

Был экспериментально получен закон, связывающий силу тока и напряжение (закон Ома). Коэффициент в этом законе назвали сопротивлением электрическому току.

Раньше ученые работали только с постоянным током и только со средами, чье сопротивление электричеству не зависит от силы тока, напряжения, времени и условий, то есть постоянно. Сейчас представления усложнились, но для постоянного тока и постоянного сопротивления по-прежнему верен закон Ома:

[Сила тока, А] = [Напряжение, В] / [Сопротивление, Ом]

Говорят, что проводник имеет сопротивление один Ом, если при напряжении в один Вольт через него течет ток один Ампер.

Примеры задач с решением

Пример 1

Задание. Чему равно добавочное сопротивление ($R$), которое подключают к вольтметру для того, чтобы предельная величина измеряемого напряжения была увеличена в 4 раза, если внутреннее сопротивление самого вольтметра равно $R_V=5\ кОм$. Ответ запишите в омах.\textit{}

Решение. Схема подключения дополнительного сопротивления к вольтметру с целью увеличения напряжения, которое он может измерять указана на рис.1.

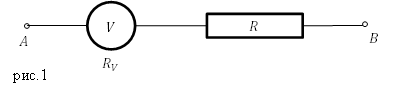
К вольтметру последовательно подключают дополнительное сопротивление. Сила тока на этом участке цепи остается без изменения, обозначим ее $I$, используя закон Ома, мы можем записать, что падение напряжения на вольтметре (рис.1) равно:

\

При этом падение напряжения на дополнительном сопротивлении составляет:

\

Падение напряжения на концах соединения AB. составляет:

\

так как по условию падение напряжения после подключения дополнительного сопротивления к вольтметру должно быть рано $4U_V$ (где $U_V=IR_V$ — падение напряжения на вольтметре при отсутствии дополнительного сопротивления).

\

Вычислим величину дополнительного сопротивления:

\

Зная, что:

\

получим:

\

Ответ. $R=15000$ Ом

Пример 2

Задание. Как можно найти сопротивление участка цепи, если известно, что при протекании по нему постоянного тока величины $I$, его мощность составляла величину $P$? В каких единицах будет выражаться сопротивление данного участка цепи?

Решение. Мощность постоянного тока величины$\ I$, который течет на участке цепи с сопротивлением $R,$ находят, используя формулу:

\

Из равенства (2.1) не составляет труда выразить сопротивление:

\

Мощность измеряется в ваттах ($\left=Вт$), сила тока в амперах ($\left=A$). Ватт является производной единицей СИ, посмотрим, какой комбинацией единиц основных величин его можно заменить:

\

Следовательно, имеем:

\=\left=\frac{\left}{\left}=\frac{кг\cdot м^2}{с^3}\ \frac{1}{А^2}=\frac{кг\cdot м^2}{с^3\cdot А^2}=Ом.\]

Ответ. Из какого закона не получали бы мы сопротивление, всегда в системе СИ единицами его измерения должен быть Ом.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Что нам дает параллельное и последовательное соединение?

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга

Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя

Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

В общем, это наиболее распространенные варианты использования этих соединений.

Цветовая маркировка резисторов

Цветовая маркировка немного упростила процесс маркировки в масштабах массового производства, но также и запутала некоторых радиолюбителей, но на самом деле все просто.

Стартовой точкой отчета принято считать золотую полоску или же серебряную – это начальное звено, и оно не считается, необходимо повернуть сориентировать таким образом, чтобы цветные полоски начинались с левой стороны.

Далее считывает номер по полоскам:

• • 0-черный;
  • 1-коричневый ;
  • 2-Красный ;
  • 3-Оранжевый ;
  • 4-Желтый ;
  • 5-Зеленый ;
  • 6-Синий ;
  • 7-Фиолетовый ;
  • 8-Серый ;
  • 9-Белый.

Третья полоса в штрих коде имеет немного иное значение – она отмеряет количество нулей, которые необходимо добавить к полученному значению. Следовательно, черный – 0, коричный – 1 ноль (0), красный – 2 нуля (00) и так далее.

Чтобы упростить себе подсчеты можно воспользоваться программой на компьютере которая называется Резистор 2.2 (ссылка на скачивание программы во вложении). Она упростит подсчеты и автоматически покажет мощность резистора при вводе всех полосок. Либо же воспользоваться калькулятором цветовой маркировки резистора прямо онлайн.

«Механическая работа. Механическая мощность»

Код ОГЭ 1.16. Механическая работа. Формула для вычисления работы силы. Механическая мощность.

Работа силы – физическая величина, характеризующая результат действия силы.

Механическая работа А постоянной силы равна произведению модуля вектора силы на модуль вектора перемещения и на косинус угла а между вектором силы и вектором перемещения: А = Fs cos а.

Единица измерения работы в СИ – джоуль: = Дж = Н • м. Механическая работа равна 1 Дж, если под действием силы в 1 Н тело перемещается на 1 м в направлении действия этой силы.

Анализ формулы для расчёта работы показывает, что механическая работа не совершается если:

• сила действует, а тело не перемещается;
• тело перемещается, а сила равна нулю;
• угол между векторами силы и перемещения равен 90° (cos a = 0).

Внимание! При движении тела по окружности под действием постоянной силы, направленной к центру окружности, работа равна нулю, так как в любой момент времени вектор силы перпендикулярен вектору мгновенной скорости. Работа – скалярная величина, она может быть как положительной, так и отрицательной. Работа – скалярная величина, она может быть как положительной, так и отрицательной

Работа – скалярная величина, она может быть как положительной, так и отрицательной.

1. Если угол между векторами силы и перемещения 0° ≤ а < 90°, то работа положительна.
2. Если угол между векторами силы и перемещения 90° < a ≤ 180°, то работа отрицательна.

Работа обладает свойством аддитивности: если на тело действует несколько сил, то полная работа (работа всех сил) равна алгебраической сумме работ, совершаемых отдельными силами, что соответствует работе равнодействующей силы.

Примеры расчёта работы отдельных сил:

Работа силы тяжести: не зависит от формы траектории и определяется только начальным и конечным положением тела: A = mg(h1 – h2)

По замкнутой траектории работа силы тяжести равна нулю.Внимание! При движении вниз работа силы тяжести положительна, при движении вверх работа силы тяжести отрицательна

Работа силы трения скольжения: всегда отрицательна и зависит от формы траектории. Если сила трения не изменяется по модулю, то её работа А = –Fтр l , где l – путь, пройденный телом (длина траектории). Очевидно, что чем больший путь проходит тело, тем большую по модулю работу совершает сила трения. Работа силы трения по замкнутой траектории не равна нулю!

Мощность N – физическая величина, характеризующая быстроту (скорость) совершения работы и равная отношению работы к промежутку времени, за который эта работа совершена: .

Мощность показывает, какая работа совершается за 1 с. Единица измерения мощности в СИ – ватт: = Дж/с = Вт. Мощность равна одному ватту, если за 1 с совершается работа 1 Дж.

Может пригодиться! 1 л. с

(лошадиная сила) ~ 735 Вт.Внимание! Для случая равномерного движения (равнодействующая сила равна нулю) при расчете мощности отдельных сил, действующих на тело, получим

Для равноускоренного движения (F = const) где ʋср– средняя скорость движения за расчётный промежуток времени.

Конспект урока «Механическая работа. Механическая мощность».

Следующая тема: «Кинетическая и потенциальная энергия» (код ОГЭ 1.17)

Сопротивление

Представьте, что есть труба, в которую затолкали камни. Вода, которая протекает по этой трубе, станет течь медленнее, потому что у нее появилось сопротивление. Точно также будет происходить с электрическим током.

Сопротивление — физическая величина, которая показывает способность проводника пропускать электрический ток. Чем выше сопротивление, тем ниже эта способность.

Теперь сделаем «каменный участок» длиннее, то есть добавим еще камней. Воде будет еще сложнее течь.

Сделаем трубу шире, оставив количество камней тем же — воде полегчает, поток увеличится.

Теперь заменим шероховатые камни, которые мы набрали на стройке, на гладкие камушки из моря. Через них проходить тоже легче, а значит сопротивление уменьшается.

Электрический ток реагирует на эти параметры аналогичным образом: при удлинении проводника сопротивление увеличивается, при увеличении поперечного сечения (ширины) проводника сопротивление уменьшается, а если заменить материал — изменится в зависимости от материала.

Эту закономерность можно описать следующей формулой:

Единица измерения сопротивления — Ом. Названа в честь физика Георга Ома.

Будьте внимательны!

Площадь поперечного сечения проводника и удельное сопротивление содержат в своих единицах измерения мм^2. В таблице удельное сопротивление всегда дается в такой размерности, да и тонкий проводник проще измерять в мм^2. При умножении мм^2 сокращаются и мы получаем величину в СИ.

Но это не отменяет того, что каждую задачу нужно проверять на то, что там мм^2 в обеих величинах! Если это не так, то нужно свести не соответствующую величину к мм^2.

Знайте!
СИ — международная система единиц. «Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».

Удельное сопротивление проводника — это физическая величина, которая показывает способность материала пропускать электрический ток. Это табличная величина, она зависит только от материала.

Похожие записи:

Руководство по правильной пайке труб из полипропилена Естественная вентиляция в частном доме Из какого материала и какую ванну лучше выбрать? обзор предложений на рынке сантехники Проточный и магистральный фильтр для воды: разновидности и модели Ножки для чугунной ванны. как выбрать и правильно установить? В какой пропорции разводить плиточный клей