Золотое сечение примеры. Как получили золотое сечение
Пропорцию золотого сечения проще всего представить, как отношение двух частей одного объекта разной длины, разделенных точкой.
Проще говоря, сколько длин маленького отрезка поместится внутри большого, или отношение самой большей из частей ко всей длине линейного объекта. В первом случае соотношение золотого сечения составляет 0,63, во втором варианте соотношение сторон равняется 1,618034.
На практике золотое сечение представляет собой всего лишь пропорцию, соотношение отрезков определенной длины, сторон прямоугольника или других геометрических форм, родственных или сопряженных размерных характеристик реальных объектов.
Первоначально золотые пропорции были выведены эмпирическим путем с помощью геометрических построений. Существует несколько способов построения или выведения гармонической пропорции:
- Классическим разбиением одной из сторон прямоугольного треугольника и построением перпендикуляров и секущих дуг. Для этого из одного конца отрезка необходимо восстановить перпендикуляр высотой в ½ его длины и построить прямоугольный треугольник, как на схеме.Если на гипотенузе отложить высоту перпендикуляра, то радиусом, равным оставшемуся отрезку, основание рассекается на два отрезка с длинами, пропорциональными золотому сечению;
- Методом построения пентаграммы Дюрера, гениального немецкого графика и геометра. Сегодня мы знаем метод золотого сечения Дюрера, как способ построения звезды или пентаграммы, вписанной в окружность, в которой как минимум четыре отрезка гармоничной пропорции;
- В архитектуре и строительстве золотое сечение чаще используется в усовершенствованном виде. В этом случае используется разбиение прямоугольного треугольника не по катету, а по гипотенузе, как схеме.
К сведению! В отличие от классического золотого соотношения, архитектурная версия подразумевает соотношение сторон отрезка в пропорции 44:56.
Если стандартный вариант золотого сечения для живых существ, живописи, графики, скульптур и античных построек рассчитывался, как 37:63, то золотое сечение в архитектуре с конца XVII века все чаще стало использоваться 44:56. Большинство специалистов считают изменение в пользу более «квадратных» пропорций распространением высотного строительства.
Золотое сечение в природе, человеке, искусстве
Прежде, чем мы начнем, хотелось бы уточнить ряд неточностей. Во-первых, само определение золотого сечения в данном контексте не совсем верно. Дело в том, что само понятие «сечение» — это термин геометрический, обозначающий всегда плоскость, но никак не последовательность чисел Фибоначчи.
И, во-вторых, числовой ряд и соотношение одного к другому, конечно, превратили в некий трафарет, который можно накладывать на все, что кажется подозрительным, и очень радоваться, когда есть совпадения, но все же, здравый смысл терять не стоит.
Однако, «все смешалось в нашем королевстве» и одно стало синонимом другого. Так что в общем и целом, смысл от этого не потерялся. А теперь к делу.
Вы удивитесь, но золотое сечение, точнее пропорции максимально приближенные к нему, можно увидеть практически везде, даже в зеркале. Не верите? Давайте с этого и начнем.
Пропорции золотого сечения в человеке
Знаете, когда я училась рисовать, то нам объясняли, как проще строить лицо человека, его тело и прочее. Все надо рассчитывать, относительно чего-то другого.
Все, абсолютно все пропорционально: кости, наши пальцы, ладони, расстояния на лице, расстояние вытянутых рук по отношению к телу и так далее. Но даже это не все, внутреннее строение нашего организма, даже оно, приравнивается или почти приравнивается к золотой формуле сечения. Вот какие расстояния и пропорции:
-
от плеч до макушки к размеру головы = 1:1.618
-
от пупка до макушки к отрезку от плеч до макушки = 1:1.618
-
от пупка до коленок и от коленок до ступней = 1:1.618
-
от подбородка до крайней точки верхней губы и от нее до носа = 1:1.618
Разве это не удивительно!? Гармония в чистом виде, как внутри, так и снаружи. И именно поэтому, на каком-то подсознательном что-ли уровне, некоторые люди не кажутся нам красивыми, даже если у них крепкое подтянутое тело, бархатная кожа, красивые волосы, глаза и прочее и все остальное. Но, все равно, малейшее нарушений пропорций тела, и внешность уже слегка «режет глаза».
Короче говоря, чем красивее кажется нам человек, тем ближе его пропорции к идеальным. И это, кстати, не только к человеческому телу можно отнести.
Золотое сечение в природе и ее явлениях
Классическим примером золотого сечения в природе является раковина моллюска Nautilus pompilius и аммонита. Но это далеко не все, есть еще много примеров:
-
в завитках человеческого уха мы можем увидеть золотую спираль;
-
ее же (или приближенную к ней) в спиралях, по которым закручиваются галактики;
-
и в молекуле ДНК;
-
по ряду Фибоначчи устроен центр подсолнуха, растут шишки, середина цветов, ананас и многие другие плоды.
Друзья, примеров настолько много, что я просто оставлю тут видеоролик (он чуть ниже), чтобы не перегружать текстом статью. Потому что, если эту тему копать, то можно углубиться в такие дебри: еще древние греки доказывали, что Вселенная и, вообще, все пространство, — спланировано по принципу золотого сечения.
Вы удивитесь, но эти правила можно отыскать даже в звуке. Смотрите:
-
Наивысшая точка звука, вызывающая боль и дискомфорт в наших ушах, равна 130 децибелам.
-
Делим пропорцией 130 на число золотого сечения φ = 1,62 и получаем 80 децибел — звук человеческого крика.
-
Продолжаем пропорционально делить и получаем, скажем так, нормальную громкость человеческой речи: 80 / φ = 50 децибел.
-
Ну, а последний звук, который получим благодаря формуле – приятный звук шепота = 2,618.
По данному принципу можно определить оптимально-комфортное, минимальное и максимальное число температуры, давления, влажности. Я не проверяла, и не знаю, насколько эта теория верна, но, согласитесь, звучит впечатляюще.
Главное, только не увлекаться этим, ведь если мы хотим что-то в чем-то увидеть, то увидим, даже если этого там нет
Вот я, например, обратила внимание на дизайн PS4 и увидела там золотое сечение =) Впрочем, эта консоль настолько классная, что не удивлюсь, если дизайнер, и правда, что-то там мудрил
Золотое сечение в искусстве
Тоже очень большая и обширная тема, которую стоит рассмотреть отдельно. Тут лишь помечу несколько базовых моментов. Самое примечательное, что многие произведения искусства и архитектурные шедевры древности (и не только) сделаны, по принципам золотого сечения.
-
Египетские и пирамиды Майя, Нотр-дам де Пари, греческий Парфенон и так далее.
-
В музыкальных произведениях Моцарта, Шопена, Шуберта, Баха и прочих.
-
В живописи (там это наглядно видно): все самые знаменитые картины известных художников сделаны с учетом правил золотого сечения.
-
Эти принципы можно встретить и в стихах Пушкина, и в бюсте красавицы Нефертити.
-
Даже сейчас правила золотой пропорции используются, например, в фотографии. Ну, и конечно, во всем остальном искусстве, включая кинематограф и дизайн.
Гармония
Гармония в саду предполагает дополнение отдельных его участков различными растениями и иными элементами в рамках единого общего. Зачастую необходимый эффект благоустройства сада достигается путем создания цветовой гармонии. Это может означать, что стилистические особенности дома повторяются в саду путем использования аналогичных строительных материалов. Единство форм, материалов и растений, a также построек создает впечатление гармонии. В качестве примера можно привести круглую мощенную камнями площадку с родезией (Rodgersia), имеющей круглые листья.
Столь же гармонично выглядят симметричные размещения растений и построек
Для этого весьма важно соблюдение пропорций
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
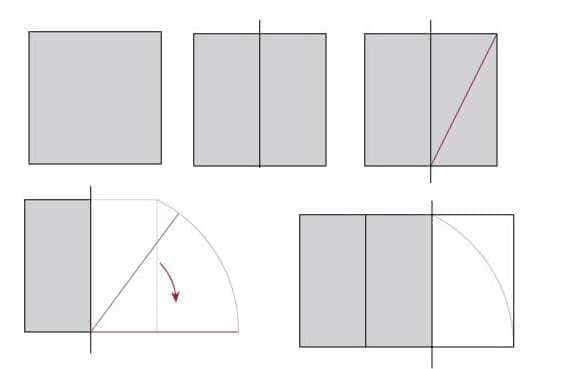
Построение прямоугольника с золотым сечением
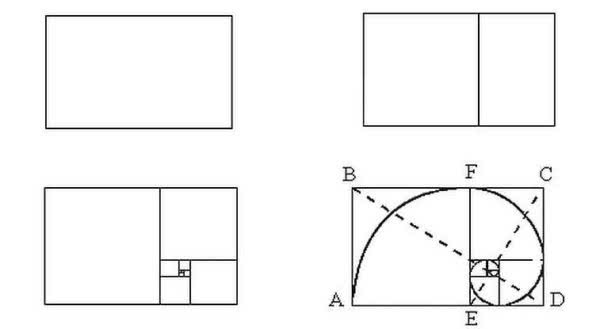
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Как построить прямоугольник с идеальными пропорциями
Чтобы применять на практике полученную информацию, надо каким-то образом научиться делить пространство или строить его согласно этому закону. Для начала давайте научимся строить прямоугольник с идеальными пропорциями. За основу берем квадрат.
Построение прямоугольника с золотым сечением
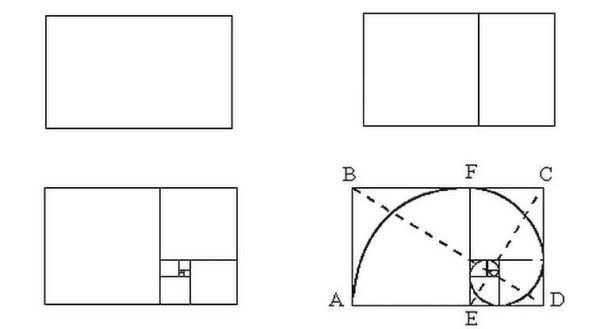
Квадрат делим пополам, в одном из полученных прямоугольников проводим линию, которая соединяет противоположные углы. Дальше берем циркуль, ставим иголку в центр нижней стороны квадрата, откладываем длину полученной диагонали и отмечаем ее на линии, которая будет продолжением нижней стороны квадрата. Полученный прямоугольник имеет соотношение сторон 1,62 (это как раз то соотношение, которое и дает 62% и 38%).
Это явно неспроста. Хотя далеко не все подчиняется этой закономерности
Что еще интересно, что если вы начнете делить прямоугольник с соотношением сторон 1,62 на квадрат и прямоугольник, вы получите снова прямоугольник с идеальными пропорциями, но меньшего размера. Если вы его снова разделите по тому же принципу, будет еще одна пара квадрат+прямоугольник со сторонами, соотношение которых будет соответствовать золотому сечению. И так до тех пор, пока вы сможете проводить деление. Но что еще интереснее, в это деление отлично вписывается ряд Фибоначчи, который имеет вид раскручивающейся спирали. Иллюстрация на рисунке выше.
Использование золотого сечения в дизайне
Принципы использования универсальной пропорции все чаще используют при строительстве частных домов
Особое внимание уделяется соблюдению оптимальных пропорций конструкции. Немало внимания уделяют правильному распределению внимания внутри дома
Современная интерпретация золотого сечения уже не относится лишь к правилам геометрии и формы. Сегодня принципу гармонических пропорций подчиняются не только размеры деталей фасада, площадь комнат или длины фронтонов, но и цветовая палитра, используемая при создании интерьера.
Соорудить гармоничное строение на модульном основании гораздо проще. Многие отделения и помещения в этом случае выполняются как отдельные блоки. Они проектируются в строгом соответствии с гармоническим правилом. Возвести здание как набор отдельных модулей, значительной проще, чем создавать единую коробку.
Многие фирмы, занимающиеся сооружением загородных домов, при создании проекта соблюдают гармоническое правило. Это позволяет создать у клиентов впечатление, что конструкция здания детально проработана. Такие дома обычно описывают, как наиболее гармоничные и комфортные в использовании. При оптимальном выборе площадей комнат жильцы психологически ощущают успокоение.
Если дом возведен без учета гармонических пропорций, можно создать планировку, которая будет по соотношению размеров стен приближена к показателю 1:1,61. Для этого в комнатах устанавливают дополнительные перегородки, или переставляют предметы мебели.
Аналогично меняют габариты дверей и окон таким образом, чтобы проем имел ширину, показатель которой меньше значения высоты в 1,61 раза.
Сложнее подбирать цветовые решения. В этом случае можно соблюдать упрощенное значение золотого сечения – 2/3. Основным цветовым фоном следует занять 60% пространства комнаты. Оттеняющий оттенок занимает 30% помещения. Оставшаяся площадь поверхностей закрашивается близкими друг к другу тонами, усиливающими восприятие выбранного цвета.
Внутренние стены комнат делят горизонтальной полосой. Ее располагают в 70 см от пола. Высота мебели должна находиться в гармоническом соотношении с высотой стен. Это правило относится и к распределению длин. К примеру, диван должен иметь габариты, которые бы оказались не меньше 2/3 длины простенка. Площадь помещения, которая занята предметами мебели, тоже должна иметь определенное значение. Она относится к общей площади всего помещения как 1:1,61.
Золотая пропорция сложно применима на практике ввиду наличия всего одного числа. Именно поэтому. Проектирую гармоничные строения, пользуются рядом чисел Фибоначчи. Благодаря этому обеспечивается разнообразие вариантов форм и пропорций деталей строения. Ряд чисел Фибоначчи также носит название золотого. Все значения строго соответствуют определенной математической зависимости.
Кроме ряда Фибоначчи, в современной архитектуре применяют и другой метод проектирования – принцип, заложенный французским архитектором Ле Корбюзье. При выборе этого способа отправной единицей измерения выступает рост владельца дома. Исходя из этого показателя рассчитывают размеры здания и внутренних помещений. Благодаря этому подходу дом получается не только гармоничным, но и приобретает индивидуальность.
Любой интерьер приобретет более завершенный вид, если в нем использовать карнизы. При использовании универсальных пропорций можно вычислить его размер. Оптимальными показателями являются 22,5, 14 и 8,5 см. Устанавливать карниз следует по правилам золотого сечения. Маленькая сторона декоративного элемента должна относиться к большей так, как относится к сложенным значениям двух сторон. Если большая сторона будет равна 14 см, то маленькую стоит сделать 8,5 см.
Придать помещению уюта можно путем деления стеновых поверхностей при помощи гипсовых зеркал. Если стена поделена бордюром, от оставшейся большей части стены следует отнять высоту карнизной планки. Для создания зеркала оптимальной длины от бордюра и карниза следует отступить одинаковое расстояние.
Применение в строительстве
Как уже говорили, неизвестно кто открыл золотое сечение, но все, что кажется нам красивым, имеет именно такое соотношение сторон. Примеров в природе очень много. Если рассматривать известные здания, то и там тоже есть та же закономерность.
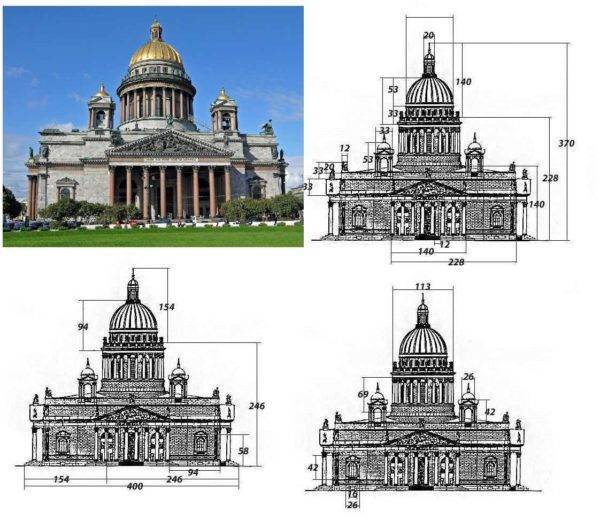
Исаакиевский собор — можете посчитать ради интереса
Если вы хотите, чтобы ваш дом внутри и снаружи был привлекательным, запоминался и нравился, при создании или выборе проекта можно просчитать хотя бы основные пропорции. Внести корректировки в пропорции, возможно, не всегда легко, часто связано с дополнительными расходами. Но, если при создании проекта сразу держать в уме золотое сечение, вопросы сами по себе отпадают. На самом деле не так уж это сложно.
Например, вы хотите дом площадью около 100 квадратных метров. Длинную сторону можно принять за 12 метров. Тогда короткая находится как 62% от длинной и составит 7,44 метра. Можно сделать 7 метров или 7,5, можно увеличить до 8. Точное, до сантиметра соблюдение размеров совсем не обязательно
Важно соотношение. А «на глаз» даже в приближении смотрится гармонично. Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов
Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно
Площадь застройки в таком случае получается несколько меньше — 90-96 квадратов. Если вам надо больше — берите длинную сторону равной 13 метрам и снова считайте. Вроде как применять золотое сечение при создании плана дома понятно.

Если основные параметры строения имеют правильную пропорцию, в любом стиле здание смотрится интересно
Высота этажа в таком случае принимается как 32% от длинной части. Она составит 12*0,32 = 3,84 метра. В принципе, это соответствует нынешним представлениям о комфортных габаритах помещения, но при желании можно сделать высоту меньше. Примерно также рассчитываются, подбираются все остальные фрагменты дома.
Не стоит забывать, что дом должен вписываться также в ландшафт. Если есть какая-то доминанта — высокий холм, например, то просчитывать надо и соотношение с холмом, и с пропорциями участка. В общем, для создания гармоничной усадьбы очень многие факторы надо учитывать.

Не только прямые линии можно использовать. Правда с изогнутыми поверхностями работать сложнее, да и обходятся они дороже — нестандартное устройство всегда более затратное
По такому же принципу разрабатывают внутреннюю планировку, стараясь по возможности соблюдать требуемое соотношение. Но еще раз повторим: по возможности. Не зацикливайтесь на точном соответствии до сантиметра. Важна общая тенденция.
Пропорции в задачах
Итак, мы обсудили:
- Когда появляется пропорция.
- Какие арифметические действия мы можем с ней выполнять.
Осталось обсудить последний вопрос: как пропорция помогает нам решать задачи?
У пропорции члена. Если три известны, а один нет, то мы можем его найти. Причем нет большой разницы, какой именно член неизвестен: , или , или , или .
Пример 1. Найти неизвестный член пропорции .
1. Первый способ.
Перемножим крест-накрест:
Выразим :
2. Второй способ
После того как мы сократили правую дробь, поменять местами средние члены:
И сразу получаем ответ:
Ответ: .
Пример 2. Найти неизвестный член пропорции: .
Перемножим крайние и средние члены:
Ответ: .
Использование Золотого сечения
Считается, что Золотое сечение использовалось как минимум 4000 лет в изобразительном искусстве и дизайне. В более современные времена Золотое сечение можно наблюдать в музыке, искусстве и дизайне. Применяя аналогичную рабочую методологию, вы можете привнести те же ощущения дизайна в вашу собственную работу.
Давайте посмотрим на пару примеров.
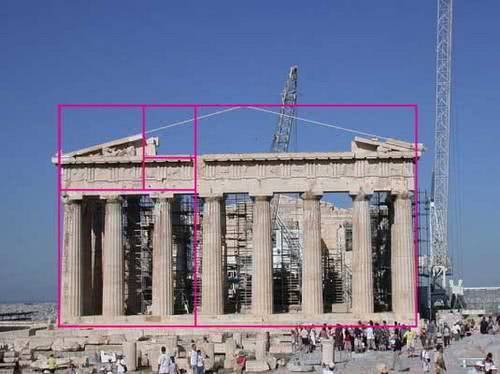
Древнегреческая архитектура использует Золотое сечение для определения нужных размеров
Древнегреческая архитектура использовала Золотое сечение, чтобы определить идеальные размерные соотношения между шириной здания и его высотой, размером портика и даже положением колонн, поддерживающих конструкцию.
Конечный результат – здание, которое ощущается полностью пропорционально. Неоклассическое архитектурное движение также повторно использовало эти принципы.

Леонардо да Винчи широко использовал Золотое сечение
Леонардо да Винчи, как и многие другие художники на протяжении веков, широко использовал Золотое сечение для создания идеальных композиций. В «Тайной вечере» фигуры располагаются в нижних двух третях (большей из двух частей Золотого сечения), и положение Иисуса идеально строится путем расположения золотых прямоугольников по всему холсту.
Есть также многочисленные примеры Золотого сечения в природе – вы можете наблюдать это вокруг себя. Цветы, морские раковины, ананасы и даже соты.
Создание золотого сечения
Создание золотого прямоугольника довольно просто, и начинается с базового квадрата. Выполните следующие действия, чтобы создать свое собственное Золотое сечение:
01. Нарисуйте квадрат

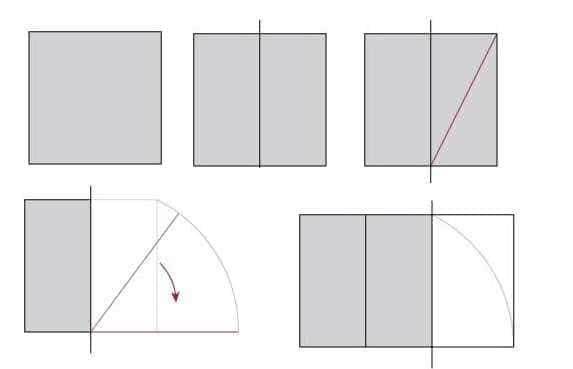
Начните с рисования квадрата любого размера. Сторона этого квадрата будет формировать длину “короткой стороны” прямоугольника.
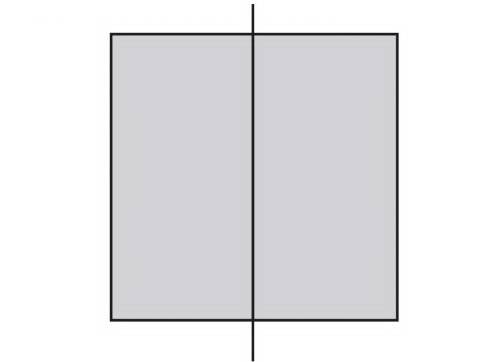
Разделите ваш квадрат пополам вертикальной линией по центру. В результате получится два прямоугольника.
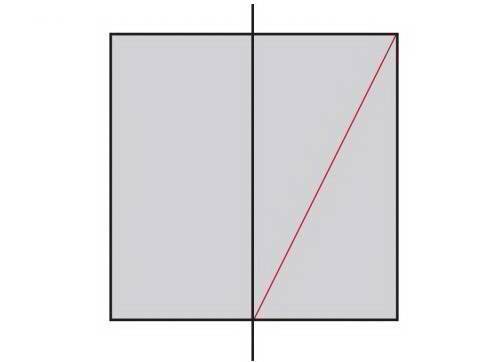
В одном из этих прямоугольников нарисуйте прямую линию от одного угла до противоположного угла.
04. Поверните линию
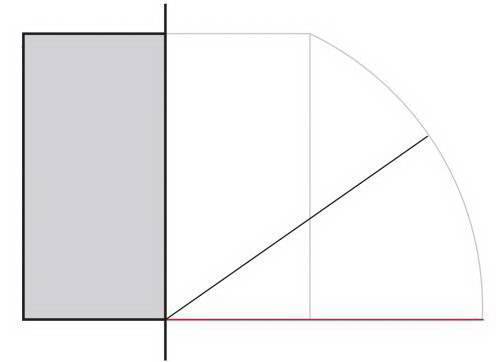
Поверните эту линию, поворачивая от нижней (или верхней) точки, пока она не совпадет с нижней частью первого прямоугольника.
05. Создайте новый прямоугольник
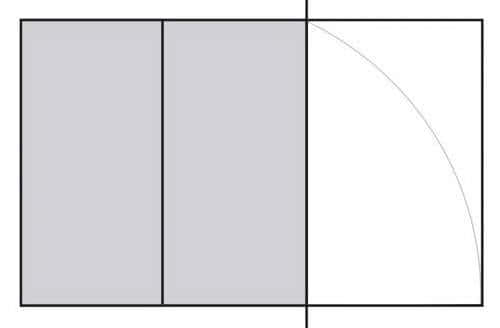
Создайте прямоугольник, используя новую горизонтальную линию и исходный прямоугольник в качестве направляющих. Это будет ваш золотой прямоугольник.
Использование Золотого сечения проще, чем вы думаете. Есть несколько быстрых трюков, которые вы можете использовать, чтобы представить идею в своих макетах.
Быстрый способ
Если вы когда-либо сталкивались с «Правилом третей», вы будете знакомы с идеей, что, разделив область на равные трети как по вертикали, так и по горизонтали, пересечение линий обеспечит естественный фокус для фигуры.
Фотографов учат размещать ключевой объект на одной из этих пересекающихся линий, чтобы получить идеальную композицию, и тот же принцип можно использовать в макетах страниц, макетах веб-сайтов и в постерах.
Правило третей может быть применено к любой фигуре, если вы примените его к прямоугольнику с пропорциями приблизительно 1: 1,6, вы получите золотой прямоугольник, что делает композицию еще более приятной для глаз.
Полная реализация Золотого сечения
Если вы хотите полностью внедрить Золотое сечение в свой дизайн, вы можете сделать это, обеспечив соотношение между областью содержимого и боковой панелью (например, в дизайне веб-сайта) в соотношении 1: 1,61.
Можно округлить это число вверх или вниз на одну или две точки, чтобы получить числа с пикселями или точками. Поэтому, если у вас есть область содержимого 640 пикселей, боковая панель 400 пикселей будет достаточно хорошо соответствовать золотому сечению.

Использование Золотого сечения в макете веб-страницы обеспечивает естественный, приятный результат.
Конечно, вы также можете разделить области контента и боковой панели вверх, используя одинаковое соотношение, и связь между верхним колонтитулом, областью контента, нижним колонтитулом и навигацией также может быть разработана с использованием того же базового золотого коэффициента.
Что влияет на высоту конька?
Коньком называют горизонтальное ребро сопряжения вершин двух скатов крыши. Завышение и занижение высоты негативно влияет на эксплуатацию кровли, портит внешний вид здания. Поэтому при расчете недостаточно руководствоваться лишь собственным вкусом
Перед тем как рассчитать высоту конька важно обратить внимание на различные технические условия
В статье примем по умолчанию крыши с равными скатами по длине и углу наклона. Это упростит определение высоты, хотя все описанные принципа применимы и к асимметричным конструкциям.
Теперь пройдемся по каждому пункту более подробно.
Кровельное покрытие
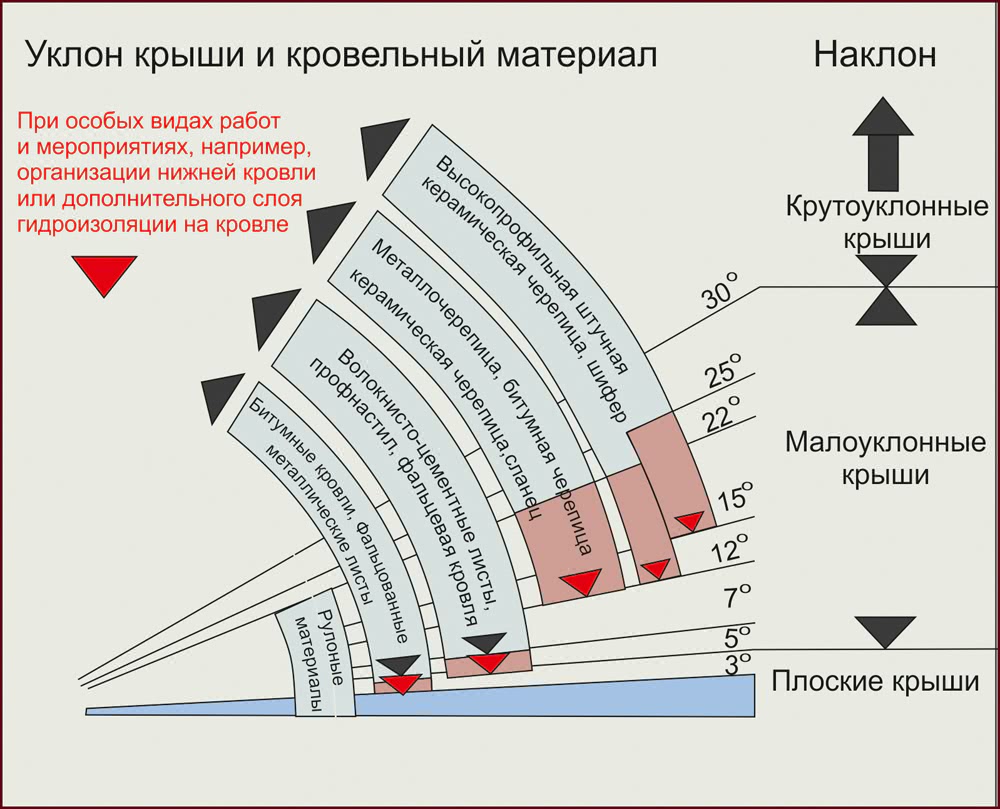
Для разных материалов есть собственные требования по крутизне уклона. От этого показателя будет зависеть расчет высоты конька двускатной крыши. Есть общие принципы выбора материал в зависимости от угла ската:
- Для небольших штучных элементов уклон ската должен быть больше чем для длинных листовых материалов. Это связано с тем, что при скапливании влаги в стыках могут появиться протечки. Поэтому коньки для шиферной крыши выше чем коньки на крышу из металлочерепицы. Дело в том, что длина волнового шифера всего 1,75 м, а металлический кровельный материал может занимать всю длину ската.
- Высота коньковой крыши влияет и на количество стыков. С занижением угла должно уменьшаться и количество соединений, нахлестов. Поэтому самыми надежными вариантами считаются крупнолистовые и рулонные материалы.
- Тяжелые кровельные элементы размещают на крутых скатах. Крыши из шифера и керамической черепицы имеют большую массу, поэтому делают крутой уклон. Так, они не прогибают стропильные балки.
При этом стоит помнить, что чем круче уклон, тем больше материала для покрытия крыши понадобится. Так, если брать за 100% потребность для угла ската 7-10°, тогда угол в 45° потребует 150% перерасход, а угол 60° — все 200%.
Чердачное помещение

Существует две разновидности домов: с чердачным помещением и без него. Для каждого варианта есть собственные условия расчета высоты конька. Если чердачное помещение жилое, тогда к росту самого высокого владельца добавляется 30-40 см. Но лучше подумать и о гостях, сделав потолок на высоте 2,4 метра
Но важно помнить, что это только потолок, а не высота крыши. Сюда нужно будет прибавить еще полметра или больше, в зависимости от предпочтений
Если чердачное помещение нежилое, тогда высота конька рассчитывается под влиянием пожарной безопасности. Один из пунктов обязывает владельцев обеспечить сквозной проход под кровлей высотой не меньше 1,6 метра, а шириной 1,2 м. При сложных стропильных системах эти размеры могут быть сокращены на 0,4 м. Это пространство обеспечит свободный воздухообмен и проход для ремонта, осмотра.
Бесчерданые здания строятся так, что над перекрытием предыдущего этажа дополнительно возводятся стены. Например, в полумансардных зданиях высота стен увеличена на 1,4 метра. В таких конструкциях высота крыши отсчитывается от нижней грани мауэрлата. Такие конструкции подходят для климатических зон с сильными ветрами. Это делает возможным уменьшить уклон ската.
Атмосферные явления

Климатические условия напрямую влияют на высоту конька. Поэтому в разных городах имеется свой «золотой» уклон ската. К атмосферным явлениям относят следующие факторы:
- Осадки. Чем больше дождей снега в вашем регионе, тем больший уклон нужно делать. Соответственно увеличивается и высота крыши. Если пренебречь этим условием, тогда увеличивается вероятность появления протечек.
- Ветер. Для местностей с ветрами средней и малой силы нет разницы в высоте конька. А вот так, где часто дуют сильные, порывистые ветра обычно уклон кровли не превышает 10°. Это накладывает определенные ограничения на применяемые материалы. Не учитывая силу ветра, вы рискуете потерять всю конструкцию крыши.
- Количество снега. Существует отношение между крутизной уклона и количеством снега. Чем больше его выпадает зимой, тем больший угол нужно делать. Причина в увеличении нагрузки на стропильную систему. Рекомендуется отдавать предпочтение скатам уклоном больше 45°.
Определить особенности региона проживания можно обратившись в местную метеослужбу или к справочной литературе. В нормативной документации СНиП 23-01-99 или СП 20.13330.2011 есть погодные карты и рекомендации по строительству.
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.
Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
Построение пентаграммы
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
https://youtube.com/watch?v=UdW0hfSzATY
Идеальный треугольник и пентаграмма
Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например
Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.
Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.
- Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
- Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.
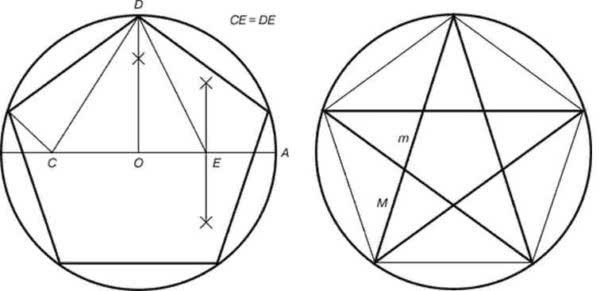
- Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
- Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.
Пропорции золотого сечения в материальном мире
В 1509 году Лука Пачоли написал книгу, которая называет число Ф «Божественной пропорцией», что было наглядно показано Леонардо да Винчи. Позже да Винчи назвал эту пропорцию золотым сечением. Оно использовалось для достижения баланса и красоты во многих картинах и скульптурах эпохи Возрождения.
Да Винчи сам использовал золотое сечение, чтобы определить все пропорции в «Тайной вечере», включая размеры стола, пропорции стен и деталей интерьера. Золотое сечение также появляется в «Витрувианском Человеке» да Винчи и «Мона Лизе». Считается, что золотое сечение использовали и другие великие художники, включая Микеланджело, Рафаэля, Рембрандта, Сьюрата и Сальвадора Дали.
Термин «фи» был придуман американским математиком Марком Барром в 1900-х годах. Ф продолжал применяться в математике и физике, в том числе в плитках Пенроуза 1970-х годов, которые позволяли мозаичным поверхностям иметь пятикратную симметрию. В 1980-х годах Ф появился в квазикристаллах – недавно открывшейся форме материи.
Фи — более чем загадочный и неясный термин в математике и физике. Он появляется вокруг нас в нашей повседневной жизни, даже в наших эстетических взглядах. Исследования показали, что когда испытуемые видят случайные лица, они считают наиболее привлекательными те, которые имеют четкие параллели с золотым сечением. Лица, оцененные как наиболее привлекательные, показывают золотые соотношения между шириной лица и шириной глаз, носа и бровей. Испытуемые не были математиками или физиками, знакомыми с правилом золотого сечения (они были просто среднестатистическими людьми), и оно вызвало инстинктивную реакцию.
Золотое сечение также проявляется во всех видах природы и науки. Ниже приведены примеры самых неожиданных мест, в которых можно его встретить.
- Цветочные лепестки. Количество лепестков на некоторых цветах соответствует последовательности Фибоначчи. С точки зрения теории Дарвина считается, что каждый лепесток помещается таким образом, чтобы обеспечить максимально возможное воздействие солнечного света и других факторов.
- Семенные головки. Семена цветка часто начинают произрастать в центре семенной головки и мигрируют наружу, заполняя свободное пространство. Например, семечки подсолнухов следуют этой схеме.
- Сосновые шишки. Семенные коробочки сосновых шишек наполнены семенами, которые растут спирально вверх, в противоположных направлениях. Количество шагов, которые делают спирали, как правило, соответствует числам Фибоначчи.
- Ветви дерева. То, как ветки дерева формируются или расщепляются, является примером последовательности Фибоначчи. Корневые системы и водоросли также придерживаются такого способа формирования.
- Раковины. Многие раковины, в том числе раковины улитки и раковины наутилуса, являются прекрасными примерами золотой спирали.
- Спиральные галактики. Млечный путь имеет несколько спиральных рукавов, каждый из которых имеет логарифмическую спираль примерно 12 градусов. Форма спирали идентична золотой спирали, а золотой прямоугольник можно нарисовать над любой спиральной галактикой.
- Ураганы. Внутреннее строение ураганов часто следует правилу золотой спирали.
- Пальцы руки человека. Каждый участок пальца от кончика основания до запястья больше, чем предыдущий, примерно на соотношение Ф.
- Тела человека и животных. Расстояние от пупка человека до пола и от макушки головы до пупка – это золотое сечение. Но человек не единственный пример золотого сечения в животном мире. Дельфины, морские звезды, морские ежи, муравьи и пчелы также демонстрируют эту пропорцию.
- Молекулы ДНК. Молекула ДНК имеет размеры 34 ангстрем на 21 ангстрем на каждом полном цикле спирали в виде сдвоенной спирали. В рядах Фибоначчи 34 и 21 являются последовательными числами.
Таким образом, примеров, где встречаются пропорции и соотношения, следующие правилу золотого сечения, более чем достаточно. Кроме перечисленных примеров, число «Фи» часто встречается в математике, физике, астрономии, биологии и иных сферах деятельности человека. Можно смело утверждать, что название «Божественное сечение» по праву присвоено числу Ф – видимо им руководствовался создатель, наполняя эту Вселенную всем живым и неживым.