Первый закон Кирхгофа
Первый закон Кирхгофа гласит, что в ветвях образующих узел электрической цепи алгебраическая сумма токов равна нулю (токи входящие в узел считаются положительными, выходящие из узла отрицательными).
Пользуясь этим законом для узла A (рисунок 1) можно записать следующее выражение:
Рисунок 1 — Первый закон Кирхгофа
I1 + I2 − I3 + I4 − I5 − I6 = 0.
Попытайтесь самостоятельно применить первый закон Кирхгофа для определения тока в ветви. На приведенной выше схеме изображены шесть ветвей образующие электрический узел В, токи ветвях входят и выходят из узла. Один из токов i неизвестен.
I1 – I2 + I3 − I4 + I5 − i = 0
I1 + I2 + I3 + I4 + I5 − i = 0
I1 + I2 + I3 − I4 + I5 − i = 0
Неправильно
Далее
Законы Ома
Для полной цепи определение будет следующим: сила тока в электроцепи равна отношению электродвижущей силы (далее ЭДС) источника к сумме сопротивлений:
I = E / (R + r),
где R – сопротивление внешней цепи, а r – внутреннее сопротивление источника тока. Довольно часто формулировка закона вызывает затруднения, поскольку не всем знакомо понятие ЭДС, ее отличие от напряжения, далеко не все знают, что означает и откуда появляется внутреннее сопротивление. Для этого и нужны пояснения, ведь закон Ома для полной цепи имеет глубокий смысл.
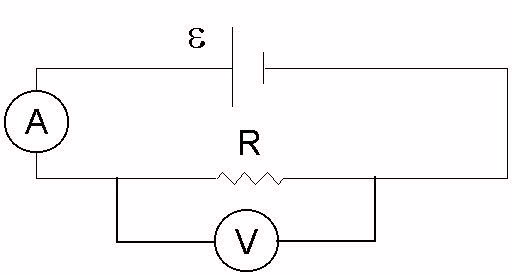
Формулировку закона для участка цепи можно назвать прозрачной. Речь идет о том, что для ее понимания не нужны дополнительные разъяснения: ток в цепи прямо пропорционален напряжению и обратно пропорционален сопротивлению:
I = U / R.
Неоднородный участок цепи постоянного тока
Определение основных параметров и процессов:
- перемещение зарядов (q) характеризуется плотностью, которая зависит от площади поперечного сечения (S) и силы тока;
- при концентрации (n) можно подсчитать количество единичных зарядов (q0), перемещенных за единицу времени;
- эту величину можно изобразить в виде цилиндрического участка проводника с объемом (V):
q = q0*n*V.
Если подключить клеммы аккумулятора к проводнику, источник питания разрядится. Для длительного поддержания процесса перемещения зарядов можно создать замкнутый в кольцо путь. Однако и в этом случае свободный дрейф электронов ограничивают совместные столкновения, противодействие зарядов молекулярной решетки материала. Чтобы компенсировать сопротивление, необходимо приложение дополнительных «сторонних» сил.
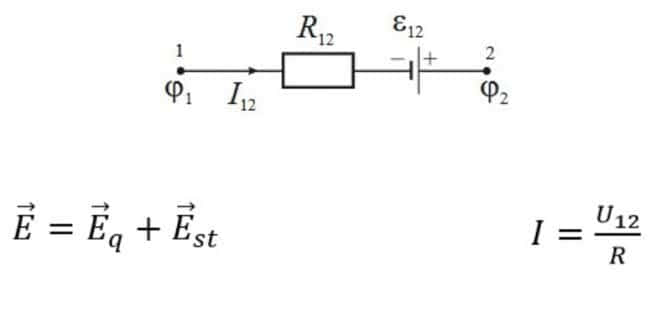
Пример неоднородного участка цепи
Рисунок демонстрирует факторы, которые следует принять во внимание. Для вычисления напряженности в любой точке этой схемы нужно суммировать векторные составляющие Eq и Est (кулоновских и сторонних сил, соответственно). Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R)
Приведенный закон Ома для неоднородного участка определяет, что сила тока (I12) = напряжение на данном участке (U12) / полное электрическое сопротивление (R).
Чтобы перенести единичный заряд q из точки «1» в точку «2», необходимо выполнить работу A12. Для этого понадобится создание определенной разницы потенциалов (ϕ1- ϕ2). Источник постоянного тока создает электродвижущую силу (ЭДС), которая способна переместить заряд по цепи. Общее напряжение будет содержать сумму перечисленных сил.
Ниже приведены формулы, характеризующие рассмотренный пример:
- A12/q = ϕ1 – ϕ2;
- Ast/q = E12;
- U = A12/q + Ast/q = ϕ1 – ϕ2 + E12;
- I = (ϕ1 – ϕ2 + E12)/ R.
Советуем изучить Гофротруба
Интегральный вариант представления рассматриваемых процессов даст аналогичный результат.
К сведению. При выполнении расчетов следует учитывать действительную полярность источника постоянного тока. В зависимости от подключения соответствующая ЭДС будет способствовать или препятствовать перемещению заряда.
Следующий пример демонстрирует решение практической задачи. Необходимо рассчитать ток в цепи, которая составлена из источника питания с ЭДС=40V и проводки с электрическим сопротивлением R=5Ом. На выходе измерены потенциалы:
ϕ1= 20V; ϕ2=10V.
Подставив значения в формулу, можно получить нужный результат:
(20-10+40)/5 = +10А.
Знак «плюс» означает, что ток идет по направлению от точки «1» к «2».
Если рассматривать процесс в дифференциальной форме, можно представить «облако», созданное из определенного количества (N) зарядов. Оно перемещается в проводнике с определенной скоростью дрейфа (Vдр). На него действуют три вида сил:
- кулоновские – Fкул;
- сторонние – Fc;
- сопротивления кристаллической решетки – Fсп.
Последний показатель будет зависеть от особенностей материала. Он может выражаться удельной проводимостью. Вектор плотности тока будет равен сумме векторов ЭДС (кулоновской и сторонней природы), деленной на удельное сопротивление.
Закон Ома для полной цепи
При рассмотрении электрической цепи мы до сих пор не принимали в расчет того, что путь тока проходит не только по внешней части цепи, но также и по внутренней части цепи, внутри самого элемента, аккумулятора или другого источника напряжения.
Электрический ток, проходя по внутренней части цепи, преодолевает ее внутреннее сопротивление и потому внутри источника напряжения также происходит падение напряжения.
Следовательно, электродвижущая сила (э. д. с.) источника электрической энергии идет на покрытие внутренних и внешних потерь напряжения в цепи.
Если обозначить E – электродвижущую силу в вольтах, I – ток в амперах, r – сопротивление внешней цепи в омах, r – сопротивление внутренней цепи в омах, U – внутреннее падение напряжения и U – внешнее падение напряжения цепи, то получим, что
E = U + U = I × r + I × r = I × (r + r),
Это и есть формула закона Ома для всей (полной) цепи. Словами она читается так: ток в электрической цепи равен электродвижущей силе, деленной на сопротивление всей цепи (сумму внутреннего и внешнего сопротивлений).
https://youtube.com/watch?v=I0VxmqzlM1E
Видео 2. Закон Ома для полной цепи
Пример 8. Электродвижущая сила E элемента равна 1,5 В, его внутреннее сопротивление r = 0,3 Ом. Элемент замкнут на сопротивление r = 2,7 Ом. Определить ток в цепи.
Пример 9. Определить э. д. с. элемента E, замкнутого на сопротивление r = 2 Ом, если ток в цепи I = 0,6 А. Внутреннее сопротивление элемента r = 0,5 Ом.
Вольтметр, включенный на зажимы элемента, покажет напряжение на них, равное напряжению сети или падению напряжения во внешней цепи.
U = I × r = 0,6 × 2 = 1,2 В.
Следовательно, часть э. д. с. элемента идет на покрытие внутренних потерь, а остальная часть – 1,2 В отдается в сеть.
Внутреннее падение напряжения
U = I × r = 0,6 × 0,5 = 0,3 В.
Так как E = U + U, то
E = 0,3 + 1,2 =1,5 В
Тот же ответ можно получить, если воспользоваться формулой закона Ома для полной цепи:
откуда
E = I × (r + r) = 0,6 × (0,5 +2) = 1,5 В.
Вольтметр, включенный на зажимы любого источника э. д. с. во время его работы, показывает напряжение на них или напряжение сети. При размыкании электрической цепи ток по ней проходить не будет. Ток не будет проходить также и внутри источника э. д. с., а следовательно, не будет и внутреннего падения напряжения. Поэтому вольтметр при разомкнутой цепи покажет э. д. с. источника электрической энергии.
Таким образом, вольтметр, включенный на зажимы источника э. д. с. показывает: а) при замкнутой электрической цепи – напряжение сети; б) при разомкнутой электрической цепи – э. д. с. источника электрической энергии.
Пример 10. Электродвижущая сила элемента 1,8 В. Он замкнут на сопротивление r =2,7 Ом. Ток в цепи равен 0,5 А. Определить внутреннее сопротивление r элемента и внутреннее падение напряжения U.
Так как r = 2,7 Ом, то
r = 3,6 – 2,7 = 0,9 Ом ;
U = I × r = 0,5 × 0,9 = 0,45 В .
Из решенных примеров видно, что показание вольтметра, включенного на зажимы источника э. д. с., не остается постоянным при различных условиях работы электрической цепи. При увеличении тока в цепи увеличивается также внутреннее падение напряжения. Поэтому при неизменной э. д. с. на долю внешней сети будет приходиться все меньшее и меньшее напряжение.
В таблице 3 показано, как меняется напряжение электрической цепи (U) в зависимости от изменения внешнего сопротивления (r) при неизменных э. д. с. (E) и внутреннем сопротивлении (r) источника энергии.
Таблица 3
Зависимость напряжения цепи от сопротивления r при неизменных э. д. с. и внутреннем сопротивлении r
| E | r | r | U = I × r | U = I × r | |
| 2 2 2 | 0,5 0,5 0,5 | 2 1 0,5 | 0,8 1,33 2 | 0,4 0,67 1 | 1,6 1,33 1 |
Для переменного тока
В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.
Импеданс, Z
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
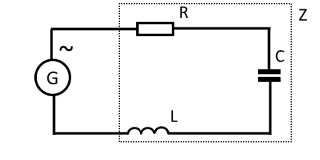 Последовательное включение R, L, C
Последовательное включение R, L, C
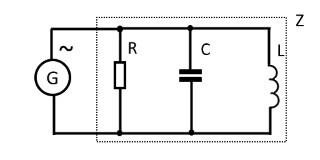 Параллельное включение R, L, C
Параллельное включение R, L, C
Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
| Импеданс, Полное сопротивление, Z | |
| При последовательном включении R, L, C | При параллельном включении R, L, C |
| Z=√(R2+(ωL-1/ωC)2) | Z=1/ √(1/R2+(1/ωL-ωC)2) |
| где, | |
| ω = 2πγ — циклическая, угловая частота; γ — частота переменного тока. |
Коэффициент мощности, Cos(φ)
Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.
Cos(φ) = P / S
Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
| I = U / Z | где | I — сила переменного тока, измеряемая в Амперах, (A) |
| U — напряжение переменного тока, измеряемое в Вольтах, (V) | ||
| Z — полное сопротивление (импеданс), измеряется в Омах, (Ω) |
Производные формулы:
| Сила тока, | I= | U/Z | P/(U×Cos(φ)) | √(P/Z) |
| Напряжение, | U= | I×Z | P/(I×Cos(φ)) | √(P×Z) |
| Полное сопротивление, импеданс | Z= | U/I | P/I² | U²/P |
| Мощность, | P= | I²×Z | I×U×Cos(φ) | U²/Z |
Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ). Скриншоты представлены на рисунках внизу:
Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)
Для постоянного тока
Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.
| I = U / R | где | I — сила тока, измеряемая в Амперах, (A) |
| U — напряжение, измеряемое в Вольтах, (V) | ||
| R — сопротивление, измеряется в Омах, (Ω) |
Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, — «Не знаешь закон Ома, — сиди дома..».
Помимо закона Ома, важнейшим является понятие электрической мощности, P:
Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.
| P = I × U | где | P — эл. мощность, измеряемая в Ваттах, (W) |
| I — сила тока, измеряемая в Амперах, (A) | ||
| U — напряжение, измеряемое в Вольтах, (V) |
Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
| Сила тока, | I= | U/R | P/U | √(P/R) |
| Напряжение, | U= | I×R | P/I | √(P×R) |
| Сопротивление, | R= | U/I | P/I² | U²/P |
| Мощность, | P= | I×U | I²×R | U²/R |
Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
Наиболее распространенные множительные приставки:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
- Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W. 1 киловатт (1 kW) = 1000 W. 1 милливатт (1 mW) = 0,001 W.
Использование на практике
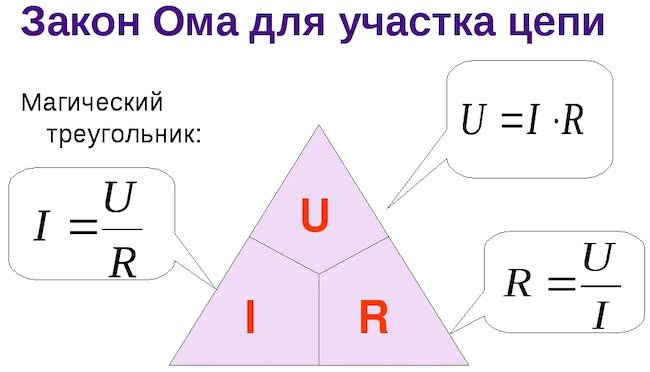
Закон Ома лежит в основе всех расчетов производимых в электронике и электротехнике. Будущих специалистов с первых дней учат, как использовать так называемый треугольник. Чтобы найти какую-то искомую величину, должны выполняться простые арифметические действия. Если два оставшихся параметра находятся в одной строке – они перемножаются. Если на разных уровнях, то верхний всегда делится на нижний.
Самые простые вычисления производятся на основе данных измерительных приборов. На участке цепи измерение тока выполняется амперметром, а напряжения – вольтметром. После этого найти сопротивление математическим путем не составит труда.
Для замеров сопротивления тоже есть прибор – омметр. Полученное выражение, подставляется в одну из формул, после чего находятся величины силы тока или напряжения. Точность омметра зависит от стабильности напряжения, подаваемого источником тока. Стабилизация проводится путем добавления резистора, выполняющего функцию регулятора.
Иногда требуется исключить из схемы какой-нибудь элемент без демонтажа. С этой целью проводится шунтирование, когда приходится устанавливать проводник на входных клеммах ненужного резистора. Ток начинает идти через шунт с меньшим сопротивлением, а напряжение на резисторе падает до нуля.
Закон Ома используется в защитных системах. Это делается с помощью уставок, обеспечивающих нормальную работу и отключающих питание лишь в аварийных ситуациях.
Закон Ома для переменного тока
При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление.В таком случае запись Закона Ома будет иметь вид:
I = U/Z
Здесь Z — полное (комплексное) сопротивление цепи — импеданс. В него входит активная R и реактивная X составляющие.Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи.Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.
С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме:— комплексная амплитуда тока. = Iampe jφ— комплексная амплитуда напряжения. = Uampe jφ— комплексное сопротивление. Импеданс.φ — угол сдвига фаз между током и напряжением.e — константа, основание натурального логарифма.j — мнимая единица.Iamp , Uamp — амплитудные значения синусоидального тока и напряжения.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит:Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.

Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
https://youtube.com/watch?v=f2rpF5ztAr0
Последовательное и параллельное включение элементов
Для элементов электрической цепи (участка цепи) характерным моментом является последовательное либо параллельное соединение.
Соответственно, каждый вид соединения сопровождается разным характером течения тока и подводкой напряжения. На этот счёт закон Ома также применяется по-разному, в зависимости от варианта включения элементов.
Цепь последовательно включенных резистивных элементов
Применительно к последовательному соединению (участку цепи с двумя компонентами) используется формулировка:
- I = I1 = I2 ;
- U = U1 + U2 ;
- R = R1 + R2
Такая формулировка явно демонстрирует, что, независимо от числа последовательно соединенных резистивных компонентов, ток, текущий на участке цепи, не меняет значения.
Соединение резистивных элементов на участке схемы последовательно один с другим. Для этого варианта действует свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U, U1, U2 – приложенное напряжение
Величина напряжения, приложенного к действующим резистивным компонентам схемы, является суммой и составляет в целом значение источника ЭДС.
При этом напряжение на каждом отдельном компоненте равно: Ux = I * Rx.
Общее сопротивление следует рассматривать как сумму номиналов всех резистивных компонентов цепи.
Цепь параллельно включенных резистивных элементов
На случай, когда имеет место параллельное включение резистивных компонентов, справедливой относительно закона немецкого физика Ома считается формулировка:
- I = I1 + I2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Не исключаются варианты составления схемных участков «смешанного» вида, когда используется параллельное и последовательное соединение.
Соединение резистивных элементов на участке цепи параллельно один с другим. Для этого варианта применяется свой закон расчета. На схеме: I, I1, I2 – прохождение тока; R1, R2 – резистивные элементы; U – подведённое напряжение; А, В – точки входа/выхода
Для таких вариантов расчет обычно ведется изначальным расчетом резистивного номинала параллельного соединения. Затем к полученному результату добавляется номинал резистора, включенного последовательно.
Интегральная и дифференциальная формы закона
Все вышеизложенные моменты с расчетами применимы к условиям, когда в составе электрических схем используются проводники, так сказать, «однородной» структуры.
Между тем на практике нередко приходится сталкиваться с построением схематики, где на различных участках структура проводников меняется. К примеру, используются провода большего сечения или, напротив, меньшего, сделанные на основе разных материалов.
Для учёта таких различий существует вариация, так называемого, «дифференциально-интегрального закона Ома». Для бесконечно малого проводника рассчитывается уровень плотности тока в зависимости от напряженности и величины удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E
Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ
Однако эти примеры скорее уже ближе к школе высшей математики и в реальной практике простого электрика фактически не применяются.






