Зачем нужно вычислять площадь аортального клапана?
Однако данный показатель важен не только для того, чтобы определить наличие или отсутствие аортального стеноза. Необходимо отметить, что нормальная работа клапанов имеет значение в любом возрасте. А патологии развития сердечной мышцы способны серьёзно повлиять на функционирование всего организма в комплексе. Поэтому такие данные могут понадобиться для того, чтобы прояснить диагноз, как касающийся работы сердечно-сосудистой системы, так и совершенно с нею не связанный.
Далеко не все знают, но иногда длительные заболевания дыхательных путей, которые не могут вылечить, тоже обусловлены слабостью сердца. Если наш «мотор» плохо качает кровь, то велик риск возникновения проблем с газообменом. А это, в свою очередь, сказывается на работе лёгких. Также не стоит забывать о том, что кровь, которая слишком слабо двигается по организму, не будет в надлежащей степени питать ткани. И это чревато снижением местного иммунитета, застойными явлениями, увеличением риска гангрены.
Поэтому обращать внимание на такой показатель объективно нужно. Данный калькулятор может стать отличным помощником для врачей, которые перепроверяют полученные сведения
С его помощью будет легче обработать информацию в большом объёме. Не менее полезен калькулятор и для студентов, решающих соответствующие задачи.
Определение величины
Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.
По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.
На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».
https://youtube.com/watch?v=2vFZ3vnV3RI
https://youtube.com/watch?v=JfcW7XIG_lI
Как найти площадь круга через длину окружности
Для начала вспомним, как вычисляется длина окружности. Здесь, как и в других формулах для круга и окружности используется постоянная π. Нужно запомнить, что в математике и физике этот символ является непременным участником всех вычислений, связанных с кругом, окружностью, циклическими процессами, движением по дуге. В частности, длину окружности находим по формулам L=2 πR, или L= πD. Используя их, находим:
R=L/2 π; (1)
D=Lπ. (2)
Используя запись 1 в формуле S = π∙r2 получаем:
S = π(L/2 π)2 = L/4 π.
Аналогичный результат получим, используя формулу 2.
Как вычислить площадь круга, описанного вокруг правильного многоугольника
В каждый круг легко вписать любой правильный многоугольник. Рассмотрим случаи с самыми простыми фигурами. Если в круг вписан квадрат, то формула будет выглядеть так:
S=2π⋅a2/2, где а – сторона квадрата.
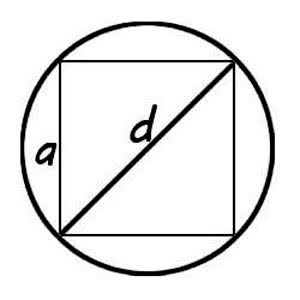
Если в круг вписан равносторонний (правильный) треугольник, то формула будет выглядеть так:
S=π⋅a2/3.
Если в равностороннем треугольнике неизвестна длина стороны, но известна высота, то используем формулу:
S=π⋅(2⋅h/3)2.
Если треугольники неправильные, например, равнобедренные или разносторонние, то формулы получаются сложнее. Например, для вычисления площади по данным равнобедренного треугольника используется формула:
S=π⋅( a4/4⋅a2−b2)
В случае прямоугольного треугольника, мы используем формулу:
S=π/4⋅(a2+b2).
Если круг описан вокруг равнобедренной трапеции, то рассчитать площадь можно по более сложной формуле:
S=π⋅( a⋅d⋅c/4⋅√p⋅(p−a)⋅(p−d)⋅(p−c)).
Как видим, задачу вычисления площади круга можно решить при помощи готовых формул, рассчитанных практически для любого случая, используя вписанные или описанные простые геометрические фигуры. Приведем еще несколько из готовых формул, на этот раз, для фигур, внутри которых находится круг неизвестного радиуса:
S=π⋅a2/12 – для равностороннего треугольника;
S=π⋅b2/4⋅(tgα/2)2 — для равнобедренной трапеции;
S=π⋅(а/2)2=π⋅а2/4 — для квадрата.
Учитывая небольшой объем статьи, все формулы приводим без доказательств, как руководство для практического использования при решении геометрических или технических задач.
Часто возникает проблема определения площади полукруга. Это можно сделать очень просто, вычислив площадь полного круга и разделив ее на 2. Если использовать формулу, то выглядеть это будет так:
S = π∙r2/2, или
S= π∙ D2/4/2 = S= π∙ D2/8.
Для решения практических задач сложно пользоваться формулами, да и времени для этого найти не всегда получается. Лучше всего воспользоваться онлайн-калькуляторами на специализированных сайтах
Здесь важно правильно замерить нужные параметры в требуемых единицах. Нот для учеников и студентов такие сервисы не подходят — легкое получение готового результата отучает мыслить самостоятельно и никак не углубляет знаний
Выбор по таблице
Зная диаметр провода, можно определить его сечение по готовой таблице зависимости. Таблица расчета сечения кабеля по диаметру жилы выглядит таким образом:
| Диаметр проводника, мм | Сечение проводника, мм2 |
| 0.8 | 0.5 |
| 1 | 0.75 |
| 1.1 | 1 |
| 1.2 | 1.2 |
| 1.4 | 1.5 |
| 1.6 | 2 |
| 1.8 | 2.5 |
| 2 | 3 |
| 2.3 | 4 |
| 2.5 | 5 |
| 2.8 | 6 |
| 3.2 | 8 |
| 3.6 | 10 |
| 4.5 | 16 |
Когда сечение известно, можно определить значения допустимых мощности и тока для медного или алюминиевого провода. Таким образом удастся выяснить, на какие параметры нагрузки рассчитана токопроводящая жила. Для этого понадобится таблица зависимости сечения от максимального тока и мощности.
| В воздухе (лотки, короба,пустоты,каналы) | Сечение,кв.мм | В земле | |||||||||
| Медные жилы | Алюминиевые жилы | Медные жилы | Алюминиевые жилы | ||||||||
| Ток. А | Мощность, кВт | Тон. А | Мощность, кВт | Ток, А | Мощность, кВт | Ток. А | Мощность,кВт | ||||
| 220 (В) | 380 (В) | 220(В) | 380 (В) | 220(В) | 380 (В) | 220(В) | |||||
| 19 | 4.1 | 17.5 | 1,5 | 77 | 5.9 | 17.7 | |||||
| 35 | 5.5 | 16.4 | 19 | 4.1 | 17.5 | 7,5 | 38 | 8.3 | 75 | 79 | 6.3 |
| 35 | 7.7 | 73 | 77 | 5.9 | 17.7 | 4 | 49 | 10.7 | 33.S | 38 | 8.4 |
| *2 | 9.7 | 77.6 | 37 | 7 | 71 | 6 | 60 | 13.3 | 39.5 | 46 | 10.1 |
| 55 | 17.1 | 36.7 | 47 | 9.7 | 77.6 | 10 | 90 | 19.8 | S9.7 | 70 | 15.4 |
| 75 | 16.5 | 49.3 | 60 | 13.7 | 39.5 | 16 | 115 | 753 | 75.7 | 90 | 19,8 |
| 95 | 70,9 | 67.5 | 75 | 16.5 | 49.3 | 75 | 150 | 33 | 98.7 | 115 | 75.3 |
| 170 | 76.4 | 78.9 | 90 | 19.8 | 59.7 | 35 | 180 | 39.6 | 118.5 | 140 | 30.8 |
| 145 | 31.9 | 95.4 | 110 | 74.7 | 77.4 | 50 | 775 | 493 | 148 | 175 | 38.5 |
| ISO | 39.6 | 118.4 | 140 | 30.8 | 97.1 | 70 | 775 | 60.5 | 181 | 710 | 46.7 |
| 770 | 48.4 | 144.8 | 170 | 37.4 | 111.9 | 95 | 310 | 77.6 | 717.7 | 755 | 56.1 |
| 760 | 57,7 | 171.1 | 700 | 44 | 131,6 | 170 | 385 | 84.7 | 753.4 | 795 | 6S |
| 305 | 67.1 | 700.7 | 735 | 51.7 | 154.6 | 150 | 435 | 95.7 | 786.3 | 335 | 73.7 |
| 350 | 77 | 730.3 | 770 | 59.4 | 177.7 | 185 | 500 | 110 | 379 | 385 | 84.7 |
Перевод ватт в киловатты
Чтобы правильно воспользоваться таблицей зависимости сечения провода от мощности, важно правильно перевести ватты в киловатты. 1 киловатт = 1000 ватт
Соответственно, чтобы получить значение в киловаттах, мощность в ваттах необходимо разделить на 1000. Например, 4300 Вт = 4,3 кВт
1 киловатт = 1000 ватт. Соответственно, чтобы получить значение в киловаттах, мощность в ваттах необходимо разделить на 1000. Например, 4300 Вт = 4,3 кВт.
Область применения
Круг — одна из фундаментальных фигур, которые окружают человека повсюду. Трубы, колеса, лампы, конфорки у плиты — всё это имеет форму круга или поперечное сечение в виде круга. Расчёт площади такого сечения может понадобиться в следующих ситуациях:
- Определение объемов емкостей.
- Решение задач по сопротивлению материалов и электротехнике.
- Расчет количества материалов при проектировании, строительстве и ремонте.
- Ведение поливного земледелия.
Стоит обратить внимание на разницу между кругом и окружностью. Окружность — это замкнутая кривая, все точки которой равно удалены от центра, в то время как круг — это часть плоскости (геометрическая фигура), ограниченная окружностью
Круг имеет ряд характеристик:
- радиус (r/R) — отрезок, соединяющий центр фигуры с его границей;
- диаметр (d/D) — отрезок, который соединяет две точки границы круга и проходит через его центр;
- длина окружности (C/c/L/l).

Таблица диаметров и сечения проводов
Формула для расчёта диаметра достаточно проста и выдаёт стандартные значения для конкретного диаметра. Поэтому часто можно увидеть в продаже соответствующие таблицы площадей круга.
Таким способом можно пользоваться в том случае, если под рукой оказался стандартный проводник, указанный в ГОСТ. Например — при диаметре сердечника 2.8 мм площадь его сечения составит 6 мм2.
Прочитав эту статью, любой человек сможет самостоятельно рассчитать площадь поперечного сечения провода или кабеля. Это пригодится при замене старой проводки или при монтаже новой кабельной линии. Главное условия подбора – повышенная точность, так как идеального соотношения качества, простоты установки, безопасности и оптимальной цены можно добиться только после проведения кропотливых замеров.
https://youtube.com/watch?v=59SGnJGL2RM
Калькулятор площади аортального клапана
Формула расчета:
Площадь аортального клапана = диаметр ВОЛЖ2 * 0,78540 * ВОЛЖ ИСК/ ИСК аортального клапана
ПСА = (ВОЛЖ) см2 = 0,785 * Диаметр ВОЛЖ
УО = 0,785 * Диаметр2 * ИСК (ВОЛЖ)
- ВОЛЖ – Выводной отдел левого желудочка
- ИСК – Интеграл скорости кровотока
- ПСА – Поперечное сечение аорты
- УО – Ударный объем
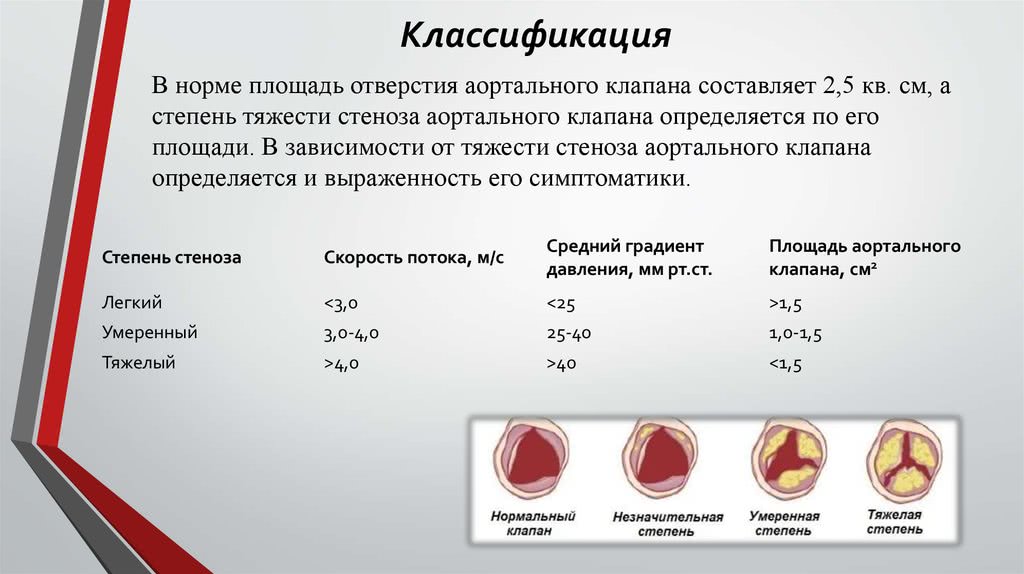
Расчет площади аортального клапана является одним из методов определения площади от клапана аорты (аортальный клапан область). Расчетная площадь отверстия аортального клапана в настоящее время является одним из критериев оценки степени стеноза аорты. Площадь клапана менее 1,0 см2 считается тяжелым стенозом аорты.
Пример расчета площади аортального клапана:
Если ВОЛЖ – 1, ВОЛЖ (ИСК) – 2 см и ИСК аортального клапана – 3 см
- ПСА = 0,785*1 = 0,785 см2
- УО = 0,785*12*2 = 1,570 см3
- Площадь аортального клапана (ПАК) = 12*0,78540*2/3 = см2
Следовательно, наблюдается серьезный риск аортального стеноза.
От стабильной работы сердечных клапанов во многом зависит продолжительность жизни человека и то, с какой именно нагрузкой он сможет справиться. Причём эти показатели серьёзно влияют на состояние здоровья и самочувствия людей в пожилом возрасте. И площадь аортального клапана – это одна из критически важных характеристик, по которой проводят диагностику такого распространённого заболевания как аортальный стеноз.
Стоит отметить, что данная патология является самой часто встречающейся среди всех нарушений, которые затрагивают аортальные клапаны в развитых странах. Это заболевание касается примерно 2% населения, находящегося в возрасте 70-80 лет. После 80 соответствующая цифра увеличивается до 3-9%. Такая разница в показателе связана с тем, что на уровень рисков влияют: пол, профессия, наличие хронических заболеваний, сказывающихся на состоянии сердечно-сосудистой системы.
Способы расчета
Чтобы получить круглое поперечное сечение, необходимо разрезать объёмную фигуру перпендикулярно оси вращения. В случае с цилиндром площади всех поперечных сечений будут равны между собой — как, например, кружки колбасы, нарезанные поперек батона, одинаковы.
Шар, по сути, представляет собой напластование блинчиков-кругов различного диаметра от точечного до заданного и обратно до точки. Чтобы найти S какого-либо из блинчиков, необходимо определить его радиус. Принцип его расчёта сводится к решению теоремы Пифагора, где гипотенузой выступает радиус шара, а искомый радиус становится одним из катетов.
При расчёте площади сечений конуса необходимо найти радиус или диаметр каждого из кругов, учитывая, что в продольном разрезе конус — это равнобедренный треугольник.
Цилиндр, конус и шар — базовые объемные фигуры. Однако существуют более сложные фигуры, например, тор. Тор, или тороид, при первом приближении являет собой не что иное, как бублик или баранку. Разломив его пополам, на торцах можно увидеть два одинаковых круга. Площадь такого поперечного сечения можно получить, удвоив имеющуюся (на рисунке серая область справа). Если взять нож и рассечь баранку вдоль, на срезе получится кольцо. В случае с такой фигурой необходимо найти площадь круга по внешней окружности и вычесть из нее «дырку от бублика» (показано серым на рисунке слева).
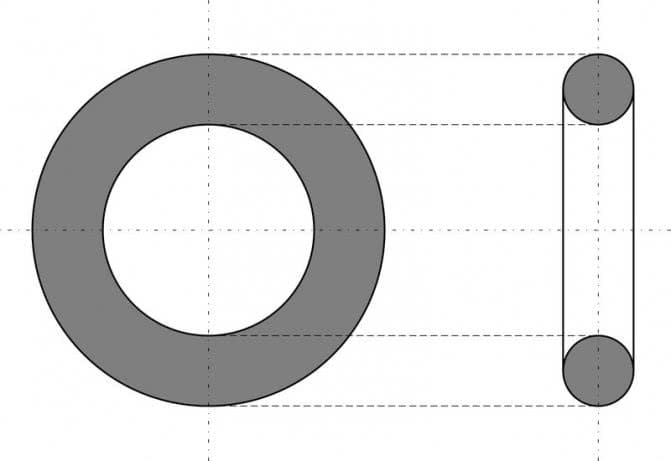
Площадь круглого поперечного сечения рассчитывается исходя из имеющихся характеристик. Она сводится к трем основным формулам. Их можно представить таким образом:
- Самая популярная, легкая в применении и часто используемая формула. Чтобы узнать площадь фигуры, если известен её радиус, нужно возвести это значение в квадрат и умножить на число π. Для бытовых расчетов достаточно двух знаков после запятой, то есть π = 3,14.
- Иногда оперируют диаметром, а не радиусом круга. В этом случае к вычислениям добавляется одна операция: диаметр умножают сам на себя, затем на число π, а произведение делят на 4.
- Если известна длина окружности С и ее радиус R и нужно выяснить площадь круга, ограниченного этой окружностью, не понадобится даже π. Используют следующую формулу: значение С делят пополам и умножают на R. Полученное чисто и будет искомой величиной.
Источники
- https://tokar.guru/hochu-vse-znat/raschet-ploschadi-poperechnogo-secheniya-kruga.html
- https://mnogoformul.ru/formuly-ploshhadi-kruga-i-raschet-onlayn
- https://www.calc.ru/ploshchad-kruga.html
- https://ru.onlinemschool.com/math/formula/circle/
- https://allcalc.ru/node/18
- https://minus-procentov-online.ru/krug/diametr/
- https://doza.pro/art/math/geometry/area-circle
- https://zen.yandex.ru/media/studystudent/dlina-okrujnosti-i-ploscad-kruga-formuly-i-primery-5e9d7c122517bd2ed0b40460
- https://2mb.ru/matematika/geometriya/ploshhad-kruga/
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Таблица с формулами площади круга
| Радиус круга r |
| Диаметр
– это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужноразделить его обратно на два.Длина окружности представляет собой удвоенное произведение радиуса и числа π:P=2πr , обратным методом получаем, чторадиус равен длине окружности , разделенной на его множитель. |
| исходные данные (активная ссылка для перехода к калькулятору) | эскиз | формула |
| 1 | радиус | |
| 2 | диаметр | |
| 3 | длина окружности | |
| 4 | сторона квадрата вписанного в круг | |
| 5 | сторона квадрата, в который вписан круг | |
| 6 | стороны треугольника | где |
| 7 | сторона равностороннего треугольника | |
| 8 | высота равностороннего треугольника | |
| 9 | боковая сторона и основание равнобедренного треугольника | |
| 10 | стороны при прямом угле треугольника | |
| 11 | боковая сторона и основание равнобедренного треугольника | |
| 12 | боковые стороны равнобедренного треугольника и угол между ними | |
| 13 | стороны прямоугольного треугольника | |
| 14 | сторона и угол при основании треугольника | |
| 15 | сторона равностороннего треугольника | |
| 16 | сторона и угол при основании трапеции | |
| 17 | боковые стороны и диагональ трапеции | где |
| 18 | стороны прямоугольника | |
| 19 | сторона и количество сторон многоугольника | |
| 20 | сторона шестиугольника |
Формулы площади круга
Площадь круга через радиус
В геометрии используются следующая формула для определения площади круга через радиус круга:
Здесь — площадь круга, — радиус круга.
В формуле фигурирует — это постоянная величина, которая называется «число » — это постоянная величина, которая часто используется в геометрии и в тригонометрии и означает отношение длины окружности к ее диаметру. Значение этого отношение получается постоянным, но не точным, и до сегодняшнего дня ученые стараются уточнить это значение. Приближенно «число » равно 3,14. Хотя после цифры «4» еще бесконечное количество цифр:
Площадь круга измеряется в квадратных единицах длины: см2, м2, дм2, мм2, кв.ед. Однако, в физике площадь круга будет рассчитываться в СИ: м2. Иногда в задачах сразу указывается — в каких единицах следует рассчитать площадь круга.
Площадь круга через диаметр
Давайте получим формулу площади круга через диаметр.
Так как диаметр — это два радиуса, то, следовательно, радиус — это половина диаметра:
— диаметр круга.
Подставим это выражение для радиуса в формулу площади круга, получим:
Таким образом, нами получена формула площади круга через диаметр круга:
Площадь круга через длину окружности
Окружность — это граница круга. Зная длину этой границы мы можем рассчитать площадь круга. Итак, формула длины окружности: , тогда определим радиус и подставим его в формулу (1):
,
И формула площади круга через длину окружности:
Длина окружности круга
Множество точек удаленных от центра круга на расстояние, не превышающее радиус круга, называется кругом. Отношение длины любой окружности C
к ее диаметруd всегда будет равно одному и тому же числу. Это число – всем известное числоπ («пи»), которое примерно равно 3,14. Так же, справедлива формула определения числаπ , как отношение длины окружностиC к двум ее радиусамr . Исходя из этого, выводится формула длины окружностиC , которая равна произведения числаπ и диаметраd окружности или 2-м ее радиусамr .
Для примера
решим простую задачу, где нужно найти длину окружности, у которой известен радиусr =2 см.
C= πd
d=2r=4 см
С=4*3,14=12,56
Подставляем известные данные в формулу длины окружности и получаем, что длина окружности примерно равна 12,56 см.






