Как найти площадь фигуры, формула

Оглавление

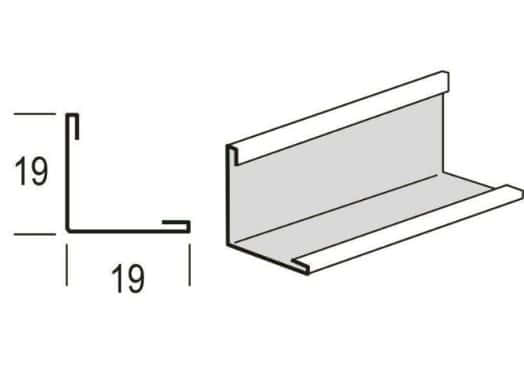
Треугольник

Формулы для нахождения площади любого треугольника представлены несколькими вариантами:

1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:

2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием. Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.

На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:

По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.

Рекомендуем: Тригонометрические формулы приведения. Подробный разбор

3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:

Для чего нужно знать площадь помещения

Первая причина проведения замеров и соответствующих вычислений — покупка строительных и отделочных материалов. Площадь пола потребуется для приобретения ламината, линолеума, ковролина. Подготовительные работы в виде стяжки, установки лаг, выравнивания основания также потребуют знания квадратуры.

Для стен считают количество штукатурки, шпаклевки, обоев. Объем краски, грунтовки также рассчитывают по отношению к квадратному метру.

Причины для нахождения площади внутренних поверхностей:

Проверить расчеты наемных работников. Часто они считают квадратуру всех отделочных работ на начальном этапе, когда на стенах нет выравнивающего слоя по маякам, чистовой шпаклевки. После проведения всех этих работ квадратура обоев и покраски значительной уменьшится.
При закладывании проводки на освещение. Определяют количество светильников в соответствии с номами освещенности.
Площадь важна при установке отопительных агрегатов, разводке радиаторных контуров. По показателям выбирают мощность приборов вентиляционной системы.

Часто приходится высчитывать площадь помещения?

Часто
80%

Редко
20%

Одни раз измерил и записал
0%

Проголосовало: 5

Расчет квадратуры стен

Проще всего посчитать результат для глухой прямой стены. В этом случае измеряют ее длину, затем высоту. Оба значения перемножают, получают искомое значение.

Особенности подсчета для сложных поверхностей:

Если на стене есть окно, дополнительно высчитывают его площадь (умножают длину на высоту), затем полученное значение вычитают из квадратуры стены.
Аналогично поступают с вертикальными поверхностями, в составе которых есть дверные проемы, арки, встроенная мебель, другие варианты.
Если стена криволинейная, например, плавно поворачивает, ее длину измеряют у пола, прикладывая рулетку так, чтобы повторить изгибы. Площадь находят, умножив протяженность на высоту.

Площади всех отдельных участков складывают, определяют общее значение.

Измерение площади ромба

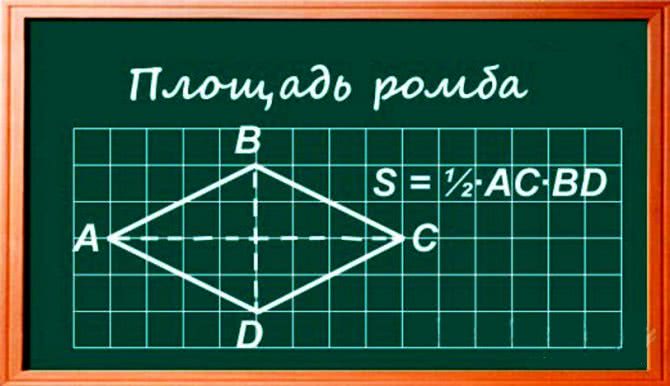
Ромб — особый вид параллелограмма, имеющий равные стороны и равные противоположные углы. Площадь ромба можно определить, используя три способа.

1. Метод высоты основания. Сначала выберите одну любую сторону в качестве базы, так как они имеют одинаковую длину. Затем определите высоту — перпендикулярное расстояние от выбранного основания до противоположной стороны.

Площадь является произведением этих двух величин и определяется по формуле: S=a×h, где: S – площадь ромба, h — высота ромба, AB=BC=AD=DC=a – сторона ромба.

2. Метод диагоналей. Другая простая формула для площади ромба, когда известны длины диагоналей. Площадь составляет половину произведения диагоналей.

В качестве формулы: S=1/2xACxBD, где: S – площадь ромба, AC– большая диагональ, BD — меньшая диагональ.

3. Использование тригонометрии. В тригонометрии, есть удобная формула, когда известны длина стороны и любой угол:

S=a2×sin α, где: S – площадь ромба, B=BC=AD=DC= a – сторона ромба, α — острый угол, β — тупой угол.

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

Калькулятор для проведения вычислений.
Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров.
Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей.
Также потребуется бумага и карандаш для ведения записей в процессе работы.

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон.

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение.
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило.

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

Определяется площадь стены без учёта двери или окна.
Вычисляется площадь каждого окна или двери путём умножения их длины на ширину.
Из площади стены вычитают площадь окон и дверей.

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их.

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении.

Несколько советов

Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем.
При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта.

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их.

Пол оригинальной формы

Первое, что следует сделать при подсчёте площади пола неправильной формы — мысленно или на бумаге расчленить его на простые фигуры. После чего высчитать отдельно площадь каждой из них и суммировать результаты.

По ходу выполнения этого задания вы обязательно заметите, что фигуры сами по себе простые, а вот процесс вычисления их площади не всегда. Для каждой отдельной части придётся применять свою формулу в зависимости от её геометрии. Некоторые из них мы сейчас рассмотрим.

Треугольники

Проще всего иметь дело с прямоугольными представителями этого семейства. Начертив его на бумаге, несложно заметить, что он составляет половину прямоугольника. Соответственно и формула расчёта отличается незначительно: S=a*b/2. Где под буквами a и b подразумевается длина катетов (сторон, соприкасающихся под прямым углом).

Если треугольник не имеет прямых углов, необходимо провести следующие действия:

принять одну из его сторон за основание;
провести от вершины к нему высоту;
умножить одно на другое;
результат разделить на 2.

В итоге формула будет иметь такой вид: S=a*h/2. Где a и h — длина основания и высота соответственно.

Для любителей экзотики существуют и другие варианты. Например, формула Герона, или подсчёт с помощью радиуса вписанной в треугольник окружности. Но проще всё-таки будет считать через основание и высоту.

Круги и овалы

Такие геометрические формы в строительстве встречаются редко, но всё же встречаются. Чтобы рассчитать площадь круга достаточно найти его радиус и подставить в уравнение: S=πr2. Оно известно нам ещё со школы. И, если верить учебникам, r — это радиус круга, а величина π равна 3,14.

Площадь овала (эллипса) вычисляется похожим образом. Только вместо радиуса необходимо найти длину двух его полуосей — длинной (a) и короткой (b). Дальше — по той же схеме: S=π*a*b.

Но чаще можно столкнуться с полукруглыми или «полуовальными» помещениями. Для подсчёта размеров такой комнаты к формулам для круга и овала в конце дописываем /2. На латыни это будет выглядеть так: S=πr2/2 и S=π*a*b/2.

Многоуровневый пол

Встречается ещё реже. И посчитать его площадь можно так, как и в примере с прилегающими помещениями — сложить показатели каждого фрагмента. Но, если вам нужно такой пол покрасить, то не забудьте учесть и вертикальные плоскости. В противном случае краски на них может не хватить.

В конце хотелось бы отметить, что главное в любых расчётах — точность. Поэтому будьте внимательны при выполнении замеров и тщательно проверяйте результаты вычислений. Это значительно упростит дальнейшие, более сложные действия во время ремонта.

4 Как рассчитать квадратуру стен

Определение площади стен часто требуется при закупке отделочных материалов — обоев, штукатурки и т.п. Для этого расчета нужны дополнительные измерения. К имеющимся уже ширине и длине комнаты нужны будут:

высота потолков;
высота и ширина дверных проемов;
высота и ширина оконных проемов.

Все измерения — в метрах, так как квадратуру стен тоже принято измерять в квадратных метрах.

Удобнее всего размеры наносить на план

Так как стены прямоугольные, то и площадь считается как для прямоугольника: длину умножаем на ширину. Таким же образом вычисляем размеры окон и дверных проемов, их габариты вычитаем. Для примера рассчитаем площадь стен, изображенных на схеме выше.

Стена с дверью:
- 2,5 м * 5,6 м = 14 кв. м. — общая площадь длинной стены
- сколько занимает дверной проем: 2,1 м *0,9 м = 1,89 кв.м.
- стена без учета дверного проема — 14 кв.м — 1,89 кв. м = 12,11 кв. м
Стена с окном:
1. квадратура маленьких стен: 2,5 м * 3,2 м = 8 кв.м.
2. сколько занимает окно: 1,3 м * 1,42 м = 1,846 кв. м, округляем, получаем 1,85 кв.м.
3. стена без оконного проема: 8 кв. м — 1,75 кв.м = 6,25 кв.м.

Найти общую площадь стен не составит труда. Складываем все четыре цифры: 14 кв.м + 12,11 кв.м. + 8 кв.м + 6,25 кв.м. = 40,36 кв. м.

4.1 Как измерять стены с дверью и окном?

Если в комнате есть окно или дверь, то для получения актуальных показателей их необходимо обязательно измерить. Воспользовавшись все той же рулеткой, узнайте высоту и ширину оконного проема, умножьте один результат на другой и вычтите это произведение из общей площади. Не надейтесь на то, что их форма является правильной.

Приведем пару примеров.

Пример 1. Стена с дверным проемом:

Общая S стены – 2,7 м х 8,0 м = 21,6 м2;
S дверного проема в стене – 2,3 м х 0,9 м = 2,07 м2;
S стены без дверей – 21,6 м2 – 2,07 м2 = 19,53 м2.

Пример 2. Стена с оконным проемом:

Общая S стены – 2,4 м х 5 м = 12 м2;
Площадь окна – 1,4 м х 1,65 м = 2,24 м2;
S стены без окна – 12 м2 – 2,24 м2 = 9,76 м2.

4.2 Что нужно, чтобы рассчитать площадь стен?

Рассчитать площадь стен дома можно либо онлайн, либо вручную. Второй вариант более трудоемкий, но точный и подходит в случае, если нет доступа к интернету по тем или иным причинам. Для расчетов потребуется:

карандаш или ручка;
листок бумаги;
калькулятор;
длинная линейка;
уровень;
рулетка.

Важно! Зная точную площадь стен и помещения, можно приобрести нужное количество строительных материалов, необходимых для ремонта. Площадь измеряют квадратными метрами и обозначают м2

На бумаге делается чертеж комнат, обозначаются окна, двери, ниши, все выступы. И по мере получения замеров, их наносят на чертеж.

4.3 Как посчитать квадратные метры стены с окном

Сложнее будет иметь дело со стеной, на которой расположено окно.

В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.

Алгоритм действий:

По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.

Важно! Цифры, которые получаются при подсчетах, обязательно записывать и обводить ручкой, чтобы не потеряться в собственных расчетах

4.4 Как посчитать квадратные метры стены с дверью

Похожие действия необходимо производить, когда требуется высчитать квадратные метры стены с дверью. Если дверь с математической точки зрения простой прямоугольник, то вычисляем ее площадь по обычной формуле А X В. То есть надо измерить высоту и длину, далее числа перемножить и получится размер двери.

Далее из площади стены вычитаем размер двери и получаем квадратуру, на которую необходимо будет покупать отделочные материалы. Если предыдущий хозяин квартиры сделал дверь с аркой, то здесь без вычисления размера круга никак не обойтись.

Площадь квадрата

Из младших классов известно, что для вычисления площади квадрата достаточно умножить его сторону саму на себя. Докажем это строго, используя лишь свойства площадей.

Попробуем вычислить площадь квадрата, если известна его сторона. Если она равна 2, то квадрат можно разбить на четыре единичных квадрата, а если она равна 3, то квадрат можно разделить уже на девять единичных квадратов:

Тогда площадь квадрата со стороной 2 равна 4, а со стороной 3 уже равна 9. В общем случае квадрат со стороной n (где n– натуральное число) можно разбить n2 единичных квадратов, поэтому его площадь будет равна n2.

Но что делать в случае, если сторона квадрата – это не целое, а дробное число? Пусть оно равно некоторой дроби 1/m, например, 1/2 или 1/3. Тогда поступим наоборот – разделим сам единичный квадрат на несколько частей. Получится почти такая же картина:

В общем случае единичный квадрат можно разбить на m2 квадратов со стороной 1/m. Тогда площадь каждого из таких квадратов (обозначим ее как S)может быть найдена из уравнения:

Снова получили, что площадь квадрата в точности равна его стороне, возведенной во вторую степень.

Наконец, рассмотрим случай, когда сторона квадрата равна произвольной дроби, например, 5/3. Возьмем квадраты со стороной 1/3 и построим из них квадрат, поставив 5 квадратов в ряд. Тогда его сторона как раз будет равна 5/3:

Площадь каждого маленького квадратика будет равна 1/9, а всего таких квадратиков 5х5 = 25. Тогда площадь большого квадрата может быть найдена так:

В общем случае, когда дробь имеет вид n/m, где m и n– натуральные числа, площадь квадрата будет равна величине

Получили, что если сторона квадрата – произвольное рациональное число, то его площадь в точности равна квадрату этой стороны. Конечно, возможна ситуация, когда сторона квадрата – это иррациональное число. Тогда осуществить подобное построение не получится. Здесь помогут значительно более сложные рассуждения, основанные на методе «от противного».

Предположим, что есть некоторое иррациональное число I, такое, что площадь квадрата (S) со стороной I НЕ равна величине I2. Для определенности будем считать, что I22>S, рассматривается абсолютно аналогично). Однако тогда, извлекая корень из обеих частей неравенства, можно записать, что

Далее построим два квадрата, стороны которых имеют длины I и R, и совместим их друг с другом:

Так как мы выбрали число R так, чтобы оно было больше I, то квадрат со стороной I является лишь частью квадрата со стороной R.Но часть меньше целого, значит, площадь квадрата со стороной I (а она равна S) должна быть меньше, чем площадь квадрата со стороной R (она равна R2):

из которого следует противоположный вывод – величина R2 меньше, чем S. Полученное противоречие показывает, что исходная утверждение, согласно которому площадь квадрата со стороной I НЕ равна I2, является ошибочным. А значит, площадь квадрата всегда равна его стороне, умноженной на саму себя.

Задание. Найдите площадь квадрата, если его сторона равна

Задание. Площадь квадрата равна 25. Найдите длину его стороны.

Решение. Пусть сторона квадрата обозначается буквой х (как неизвестная величина). Тогда условие, согласно которому его площадь равна 25, можно переписать в виде уравнения:

Его простейшее квадратное уравнение, для его решения надо просто извлечь квадратный корень из правой части:

Примечание. Строго говоря, записанное уравнение имеет ещё один корень – это число (– 5). Однако его можно отбросить, так как длина отрезка не может быть отрицательным числом. В более сложных геометрических задачах отрицательные корни также отбрасывают.

Задание. Численно площадь квадрата равна периметру квадрата (с учетом того, что площадь измеряется в см2, а периметр – в см). Вычислите его площадь.

Решение. Снова обозначим сторону квадрата как х, тогда площадь (S)и периметр (Р) будут вычисляться по формулам:

По условию эти величины численно равны, поэтому должно выполняться равенство, являющееся уравнением:

Естественно, сторона квадрата не может быть равна нулю, поэтому нас устраивает только ответ х = 4. Тогда и площадь, и периметр будут равны 16.

Ответ: 16 см2.

Обратите внимание, что ответ задачи зависит от единицы измерения. Если использовать миллиметры, то сторона квадрата окажется равной 40 мм, периметр будет равен 160 мм, а площадь составит 1600 мм2

Именно поэтому в условии задачи сказано, что площадь и периметр равны численно. «По-настоящему» равными бывают только величины, измеряемые в одинаковых единицах измерения.

Рассчитать площадь пола

По полу так же можно рассчитать площадь помещения. При этом лучше, чтобы все стены в нём и пол были свободны. Если комната прямоугольная, следует просто перемножить размеры двух сторон пола. Но даже в таком случаи, они могут иметь небольшие различия в размере, поэтому надо снять мерки со всех сторон пола. Нужно делать замеры по поверхности пола, не рекомендовано замерять по стенкам — они могут иметь неровности.

При неправильной конфигурации помещения, пол делится на правильные фигуры. После чего, считается размер каждой фигуры. Для наглядности рекомендовано нарисовать схематичный чертёж со всеми размерами. Если пол двухуровневый, его так же необходимо зонировать.

Предназначение вычислений размера пола играет важную роль. Допустим, если расчёт требуется для установки тёплого пола, то нет надобности учитывать места, где будет размещаться тяжёлая мебель. А если для определения — сколько необходимо напольного покрытия, чтобы застелить всю поверхность пола — то высчитывается размер в полном объёме.

При расчёте габаритов, нет надобности в соблюдении размеров до сантиметра, допустимо производить округления. Проверить, правильно ли вы подсчитали площадь пола можно на онлайн-калькуляторе.

Расчет площади помещения со стандартной формой

Сегодня всё чаще можно встретить комнаты с непривычной конфигурацией: треугольные, круглые или трапециобразные.

Расчёт треугольной формы

Бывают помещения по виду напоминающие треугольник. Рассчитать площадь такой комнаты в квадратных метрах доступно как на калькуляторе, так и с использованием формулы.

а — основание;
h — перпендикулярная высота.

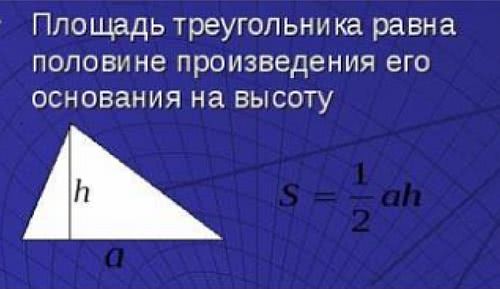
Чтобы провести расчёт, измеряется длина основания треугольника и высота, проведённая перпендикулярно основанию из противоположно расположенного угла. Единственное — проведение перпендикулярной при замере сделать не просто, особенно если не использовать специальный инструмент. Поэтому, полученные данные могут быть не точными.

Для расчёта S треугольника лучше воспользоваться формулой Герона. Она более сложная, но результат получается точнее.

a, b,с — длины сторон;
p — половина периметра (р = ½ (а + b + с)).

Так же, посчитать площадь треугольной фигуры можно на онлайн-калькуляторе.

Трапеция

Помещение, являющееся угловым, нередко имеет трапециобразную форму. Главная черта трапеции — расположение двух сторон в параллельной плоскости, а двух других — нет, они находятся под разными углами.

Для определения S трапециобразной комнаты делается замер двух параллельных сторон, и высоты — перпендикулярной линии между сторонами. Чтобы убедиться, что стороны расположены точно параллельно, нужно измерить высоту в нескольких местах.

Эти данные следует вставить в разделы калькулятора, или в формулу:

A и B — длина сторон лежащих параллельно;
h — высота.

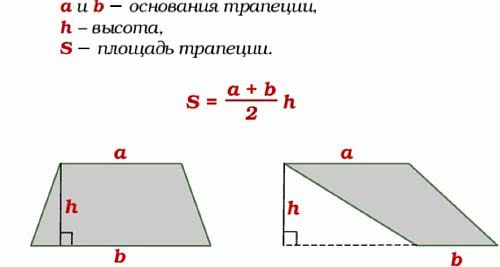
Сделать данные вычисления потребуется, если определяется размер многоугольной комнаты. Допустим, имеется 5 углов, тогда многоугольник следует разделить на две фигуры — прямоугольник и трапецию, и сделать два расчёта, а результаты сложить.

Есть еще один способ, как рассчитать площадь трапециобразной комнаты в м2 — поделить трапецию на прямоугольные и треугольные фигуры, и определить размер каждой, а затем всё сложить.

Круг

В новостройках встречаются участки здания с округлой формой (полукруг или четверть). Нередко это бывает при совмещённом балконе или эркере.

Сначала нужно определить значение выпуклой части, которое потом приплюсовывается к остальным результатам. Замеры округлых участков можно производить, используя гибкую рулетку или бечёвку.

Рассчитать S круга легко по формуле:

n – коэффициент равный 3,14;
R² — радиус круга в квадрате.

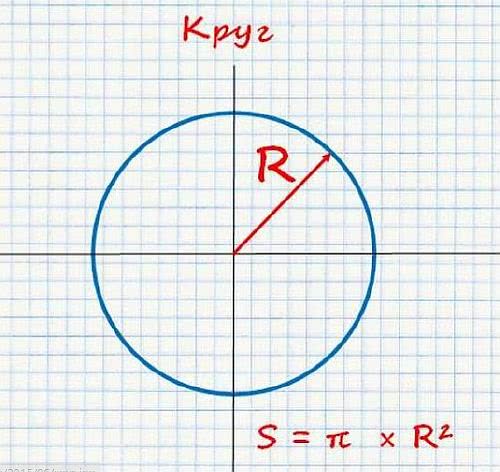
Сложнее подсчитать S отдельной части круга отсечённого хордой. Такие расчёты производятся по формуле:

Для таких вычислений подойдёт калькулятор, в нём есть специальная форма для расчёта площади круга.

Как высчитать квадратный метр: нюансы, которые следует обязательно знать

Чаще всего при указании квадратуры упаковки того или иного строительного материала производитель приводит квадратные метры. Система СИ принята во многих странах. Как рассчитать квадратный метр? Можно вычертить квадрат с метровой стороной. В этом случае поверхность, очерченная данным квадратом, и будет равна квадратному метру. Большинство измерительных приборов позволяют получить результаты измерения сразу в квадратных метрах.

Квадратный метр найти несложно

Кроме квадратных метров можно использовать и другие единицы измерения. При наличии онлайн-калькулятора расчет квадратных метров значительно упрощается. Однако при желании перевод можно выполнить самостоятельно, умножив имеющееся значение на соответствующий коэффициент, можно найти искомое значение. Для начала следует определить с новой единицей измерения. Если это:

Футы. Используем коэффициент 0,093. Такое соотношение характерно для квадратных единиц измерения. Высчитав линейные значения в футах и получив значение в футах, умножаем квадратуру на 0,093 и получаем новое значение квадратуры, выраженное в квадратных метрах. Если расчет выполнен правильно, численное выражение площади должно уменьшиться. Если к точности расчетов предъявляются повышенные требования, вместо коэффициента 0,093 лучше использовать 0,092903;

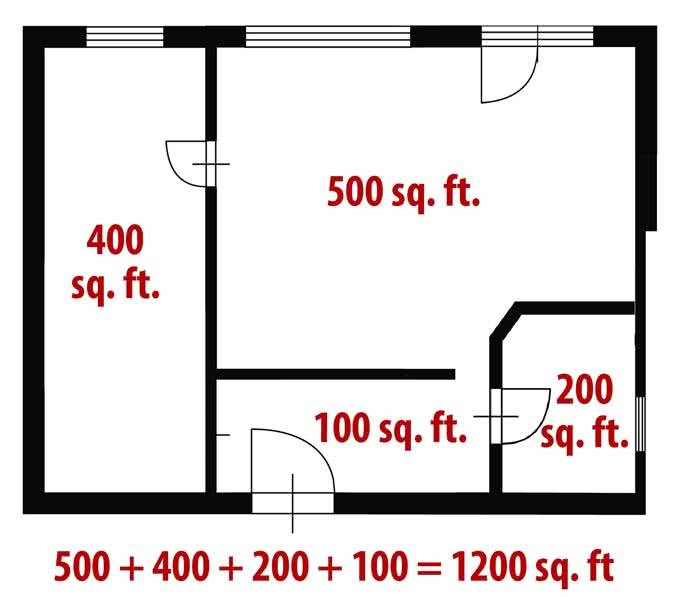
Для перевода из квадратных футов в метры умножаем на 0,093

Ярды. Коэффициент равен 0,84. Перевод ядров в квадратные метры выполняется по алгоритму, описанному выше. Для более точных расчетов можно использовать поправочный коэффициент 0,83613;
Акры. При расчете квадратуры помещения такие единицы измерения используются редко, так как один акр равен 4050 квадратным метрам. Однако при необходимости перевод можно сделать с помощью поправочного коэффициента 4050 (4046,9 при более точном расчете).

Акр используется при определении квадратуры земли

Возможно использование и других единиц

При переводе площади важно помнить, что речь идет о квадратах, а потому используется не соотношение линейных размеров, а площадей. Найти поправочный коэффициент в этом случае достаточно просто

Если известно, что метр и искомая единица измерения соотносятся как коэффициент К, то поправочный коэффициент будет численно равен К².

Как найти площадь фигуры